数字信号处理对一段信号进行进行傅里叶分析,一般需要采样,简单来说就是 截取一段数据才进行分析,然后用观察的信号时间片段进行周期延拓处理,得到虚拟的无限长的信号,然后就可以对信号进行傅里叶变换、相关分析等数学处理。
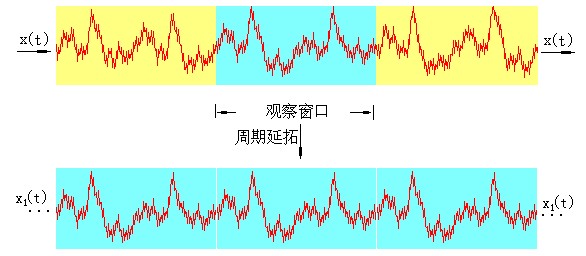
周期延拓后的信号与真实信号是不同的,下面从数学的角度来看这种处理带来的误差情况。设有余弦信号x(t)在时域分布为无限长(- ∞,∞),当用矩形窗函数w(t)与其相乘时,得到截断信号xT(t)=x(t)w(t)。根据博里叶变换关系,余弦信号的频谱X(ω)是位于ω。处的δ函数,而矩形窗函数w(t)的谱为sinc(ω)函数,按照频域卷积定理,则截断信号xT(t)的谱XT(ω) 应为

将截断信号的谱XT(ω)与原始信号的谱X(ω)相比较可知,它已不是原来的两条谱线,而是两段振荡的连续谱。这表明原来的信号被截断以后,其频谱发生了畸变,原来集中在f0处的能量被分散到两个较宽的频带中去了,这种现象称之为频谱能量泄漏(Leakage)。
信号截断以后产生的能量泄漏现象是必然的,因为窗函数w(t)是一个频带无限的函数,所以即使原信号x(t)是限带宽信号,而在截断以后也必然成为无限带宽的函数,即信号在频域的能量与分布被扩展了。又从采样定理可知,无论采样频率多高,只要信号一经截断,就不可避免地引起混叠,因此信号截断必然导致一些误差,这是信号分析中不容忽视的问题。
如果增大截断长度T,即矩形窗口加宽,则窗谱W(ω)将被压缩变窄(π/T减小)。虽然理论上讲,其频谱范围仍为无限宽,但实际上中心频率以外的频率分量衰减较快,因而泄漏误差将减小。当窗口宽度T趋于无穷大时,则谱窗W(ω)将变为δ(ω)函数,而δ(ω)与X(ω)的卷积仍为H(ω),这说明,如果窗口无限宽,即不截断,就不存在泄漏误差。
 为了减少频谱能量泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。泄漏与窗函数频谱的两侧旁瓣有关,如果两侧p旁瓣的高度趋于零,而使能量相对集中在主瓣,就可以较为接近于真实的频谱,为此,在时间域中可采用不同的窗函数来截断信号。
为了减少频谱能量泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。泄漏与窗函数频谱的两侧旁瓣有关,如果两侧p旁瓣的高度趋于零,而使能量相对集中在主瓣,就可以较为接近于真实的频谱,为此,在时间域中可采用不同的窗函数来截断信号。
常用窗函数
矩形窗
矩形窗是最常见的窗函数,默认情况就是属于矩形窗函,属于时间变量的零次幂窗,函数形式为
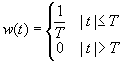 相应的窗谱为
相应的窗谱为
 矩形窗的优点是主瓣比较集中,缺点是旁瓣较高,并有负旁瓣(下图所示),导致变换中带进了高频干扰和泄漏,甚至出现负谱现象。
矩形窗的优点是主瓣比较集中,缺点是旁瓣较高,并有负旁瓣(下图所示),导致变换中带进了高频干扰和泄漏,甚至出现负谱现象。

hamming窗
hamming窗的公式为:
ω(n)=[a0−(1 - a1)cos(2π(n−1)/N)]
a0 = 0.54 和 a1 = 0.46


现在讨论下不同相位下同一频率的信号的频谱:
时域信号1:

该信号的频谱为
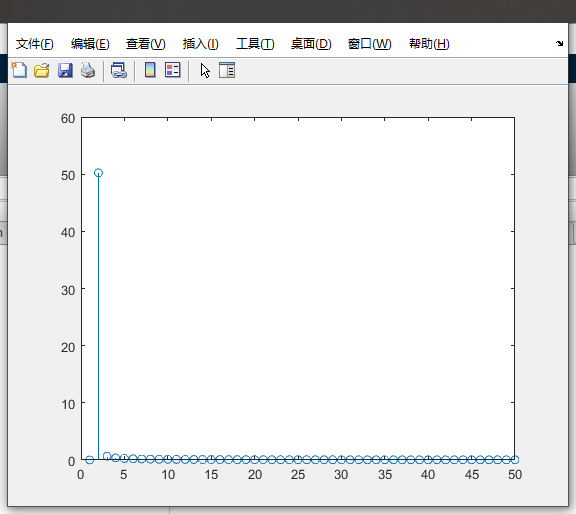
同样的周期,时序信号2为:

该信号的频谱为

由频谱可以知道,信号1的频谱非常干净,只有一根谱线,但是信号2的频谱却出现了很多的杂谱,虽然只是相位上面小小的差距,但对傅里叶变换却是致命的,一旦时域信号出现小的误差,对频域却是非常大的影响。
为了消除这类的影响,引入了短时傅里叶变换的方法,具体的方法是将一个信号分成非常多的小窗口,单独对每个窗口进行傅里叶分析,但是这样也引入了问题,当这个窗口过小时候,有些低频信号因为周期比较长无法完全在这个窗口内,因此会导致FFT的结果低频信号缺失。
正如上述所讲,窗口的选取很重要,小波分析正是窗口的选取是一个可变的过程。
语音信号特指人的发生器官发出的声音。
语音信号的组成:
说话时一次性发出的,具有一个响亮的中心,并且可以被明显感受到的叫做音节。
一个音节由一个或多个音素组成,音素(phoneme)是语音的最小单位
任何语言都有元音(vowel)和辅音(consonant)两种音素。
元音声学特性:
气流从喉腔吸入,从唇腔呼出,这些声腔完全开放,气流顺利通过,发出的声音叫元音。
辅音声学特性:
由于通路一部分闭起来或者受到阻塞,而克服这种阻塞发生器官产生音素叫辅音
半元音:
人的声道基本畅通,但是有小部分阻塞。
任何一个音节都具有元音以及辅音,元音构成了音节的主干,辅音通常主线在音节的结尾。
元音的共振峰formant特性:
当激励进入人声道会引起共振,共振峰是区分不同元音的重要参数,共振峰参数包含了共振峰频率和频带宽度,一个元音可能有多个共振峰。例如有信号频谱如下:

根据该频谱可以获得共振峰如下:

该语音信号有4三个共振峰,分别位于1K,1.8K,3.2K,4.1k处。
(正常情况下,同样的语音信号,女音的共振峰频率比男音还高,但是共振峰的形状是相同的)。
语音信号的通用分析
语音的信号的时域分析。
语音信号的时域分析常用两种方法:
假设加窗后的信号为
$$x_n(m)=w(m)*x(m+n)$$
$$w(m)=\begin{cases}
1, & \text{if $m$ = 0~(N-1)}
0, & \text{if $m$ = 其他值 }
end{cases}$$
语音信号的短时平均能量:
$$E_n=\sum_{m=0}^{N-1}{x_n}^2(m)$$
短时平均幅度
$$E_n=\sum_{m=0}^{N-1}|{x_n}(m)|$$
时域短时能量和平均幅度能够衡量很多指标:
- 可以区分清音段和浊音段,因为浊音段Em的值比清音大得多。
- 可以区分声母和韵母的边界,有声和无声的边界,连字的边界。
- 作为一种超音段信息,用于语音识别中。
短时过零率
短时过零率代表信号在窗口中穿过横轴的次数,显然高频信号具有较高的过零率,低频信号反之,利用平局过零了还可以判断寂静无声和有声段的起点和终点,在孤立词的语音识别中,需要在一连串的语音信号中进行适当的分割,来确定一个一个的孤立的单词信号,在背景音较小的时候,用平均能量来分割有效 ,在背景噪声大时,用过零率来判断较为有效,当然也可以通过两个参数合起来判断。
语谱图
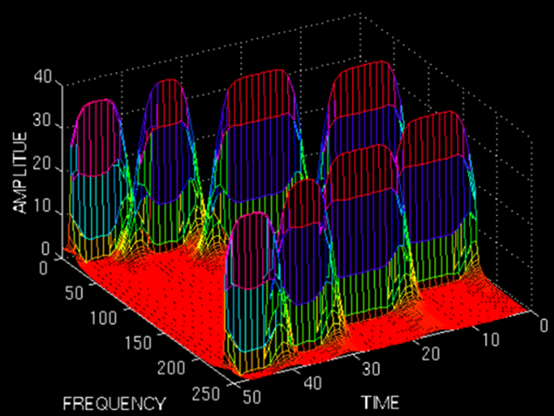
语音信号属于短时平稳信号,在10ms-30ms的范围内,一般可以认为语音信号特性基本不变,因此分析可以截取一段信号进行分析,对该信号时间分成几个小段进行傅里叶变换,就是该信号的语谱图,下图横轴表示时间,纵轴表示频率,颜色深浅表示该频率的幅度。
语谱图例子:

语谱图的横纹代码的是共振峰,代表一段时间上具有相同的频率点,横纹的长度代表了带宽。
竖纹代表的是基音,竖纹的长度代表了基音的周期。
如根据上面总结所示,横纹代表了元音,可以用于辨识元音,竖纹代表了细节,是辅音。
从上图可以看出,元音也就是横纹有一般出现在低频段。
起源
Ros最初起源于斯坦福大学人工智能实验室和机器人技术公司(Willow Garage)合作的个人机器人项目。
Ros是一套用于编写机器人软件的灵活框架,它集成了大量的工具,库,协议,提供了类似操作系统额功能,包括硬件抽象化的描述,底层驱动管理,共用功能的执行,程序间的消息传递,程序发行包管理,可以极大的简化繁杂多样化的机器人平台下复杂任务创建和稳定行为控制。
Ros组成部分:
- 通信机制
- 开发工具
- 应用功能
- 生态系统
Ros特点:
- 免费而且开源,部分允许商业化。
- 组件化工具包,意味着开源裁减。
- 点对点的设计,适应于多机器人单个控制器的场景
Ros的主流版本
ROS版本较多,各个版本之间不同是对操作系统的支持程度不一样,比如ROS kinect仅支持ubuntu16.04和15,因此安装ROS需要根据自己的ubuntu版本来选择安装对应的ros。
Ros的架构
分成三个层次:
应用层
包括master和application
中间层
包括一些第三方库,TCPROS/UDPROS,NodeLet API
OS层
主要是linux操作系统
从实现角度讲ROS分为另外三个层次

计算图
以节点为单位,每个ROS程序功能作为一个节点运行,可以分布在不同的主机。master节点统筹了多个节点的运行,提供节点发现功能,通过RPC调用的形式提供服务。
文件系统
ROS将文件按照一定的组织规则放置,分为

- 综合功能包和综合功能包清单: 综合功能包包含了多个功能包,比如一个ROS导航可能报关行韩了建模,定位,导航等多功能包。
- 功能包和功能包清单 包含了ROS节点,库,配置文件等,记录功能包的基本信息,包含作者,许可,依赖,编译标志,包含在xml功能包配置文件内。
功能包包含的文件目录
config:配置文件
include:头文件
scripts:Python脚本
src: C++代码
launch: 启动文件
CMakeLists.txt: 编译规则
package.xml: 记录功能包基本信息,该文件中<build_depend>标签内定义编译时所依赖的其他功能包,<run_depend>标签内定义运行时所依赖的其他功能包
功能包命令
catkin_create_pkg 创建功能包
rospack 获取功能包的信息
catkin_make:make 编辑工作控件中的功能包
rosdep:depend 自动安装功能包依赖的其他包
roscd:cd 包目录跳转
roscp:copy 拷贝功能包中的文件
rosed:edit 编辑功能包中的文件
rosrun 运行功能包中的可执行文件
roslaunch 运行启动文件
消息 消息是ROS节点之间发布/订阅信息的格式定义,存储在.msg文件中
一个节点可以在一个给定的主题中发布消息。一个节点针对某个主题关注与订阅特定类型的数据。可能同时有多个节点发布或者订阅同一个主题的消息。总体上,发布者和订阅者不了解彼此的存在。

服务 服务是ROS 客户端/服务器模型下的请求和应答数据类型的格式定义,存储在.srv文件中。

怎么使用ROS
ROS开发有工作空间的概念,工作空间是自己的代码和代码包的存放地点,目录格式如下

src: 用户自己的代码空间。
build: 编译空间,用来存储生成的缓存信息。
devel: 用来防止可执行文件。
创建工作空间:
$ mkdir -p ~/catkin_test/src
$ cd ~/catkin_test/src
$ catkin_init_workspace
//创建文件夹
$ cd ~/catkin_test
$ catkin_make
//编译整个ROS项目
注意ros无法自动判断代码已经修改,因此更新或者修改后需要执行clean清理之前的生成文件,不然修改无法生效
$ catkin_make clean
环境变量设置
由于ROS环境变量依赖于Linux系统环境变量
$ source devel/setup.sh
$ env | grep ROS
如果无误,应该会出现

ROS_PACKAGE_PATH应该包含ROS系统包目录和用户包目录。
前面讲述了加窗信号的能量泄露问题
还有
现在讲述傅里叶变换对于非平稳信号分析的劣势:
非平稳信号FFT
非平稳信号是指信号频率随着频率改变的信号,如下图:

那么对该信号做傅里叶变换,就是先进行周期拓展,然后再做FFT,得到频谱如下,顺带附上平稳信号的FFT进行比较:

可以看出来,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
非平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,比如生物医学信号,音频信号,在这些信号的分析中是基本看不到单纯傅里叶变换这样naive的方法。
解决非平稳信号频率分析-短时傅里叶变换 STFT

就是加窗,但是加窗会带来两个问题:
窗太窄-频率分辨率差
窗太长-时间分分辨率差
傅里叶变换的原理回顾
信号的互相关函数
两个变量f1(x)和f2(x)的相关函数为
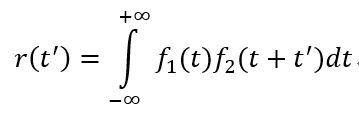
傅里叶变换的原理,就是计算各个频率分量和各个三角基频的相关性。

上面这个卷积实际上是计算相关性的一个过程
高频

低频

小波变换的原理
小波变换并不是在单纯的STFT的基础上,通过算法改变STFT的窗口实现的,回顾上面的傅里叶信号原理,小波是通过修改采样函数的基从无限的余弦函数为有限的小波函数实现的
小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。

小波函数

不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。
因此,不同于傅里叶变换,小波变换的结果并不是代表频谱,小波变换的某个点代表这个时间段,这个频率有某个"小波"。因为小波变换的基不是周期三角函数,而是一个一个"小波"。
小波变换的结果示意
小波变换和短时傅里叶变换的差别在于小波的时间分辨率是可调的。
小波变换提供了两个尺度的信号分析结果-时间,频率。
小波的含义,即为时间上衰减快,和傅里叶的正弦波相比要短。
小波变换的过程:
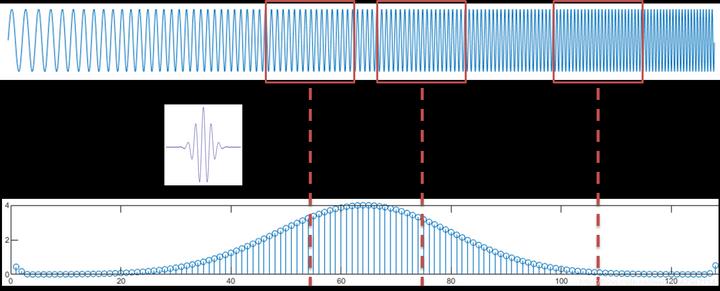
在时间域上,可以通过小波在时间上的移动,逐一比较不同位置的窗口信号,得到小波系数,小波系数越大,则证明小波与该段信号的拟合程度越好。计算中用小波函数与该窗口信号的卷积,作为该窗口下的小波系数。窗口的长度和小波的长度是相同的。
在频率域上,通过拉伸或压缩小波的长度,来改变小波的长短和频率,实现不同频率下的小波系数。相应的,窗口长度也会随着小波长度变化。由于高频处小波被压缩,时间窗变窄,使得时间分辨率更高。
将不同频率下的小波系数组合起来,便得到了时频变换的小波系数图。

从图上可以看到,低频处频率分辨率要好于高频处的。小波时频图的特点为整体呈现高频处高而瘦,低频处矮而宽。
小波中,一般用尺度scale来衡量小波的频率f,两者之间的转换关系为:

公式中,Fs代表信号的采样频率,wcf为小波的中心频率(wave central freq),在matlab里可以用 centfrq(wavename) 来查询。
cwt的原理很简单,就是用不同尺度的小波逐个窗口去卷积,得到小波系数矩阵。所以根据原理,可以自己编程实现小波变换,比如:
fs=2^6; %采样频率
dt=1/fs; %时间精度
timestart=-8;
timeend=8;
t=(0:(timeend-timestart)/dt-1)*dt+timestart;
L=length(t);
z=4*sin(2*pi*linspace(6,12,L).*t);
%定义计算范围和精度
fmin=2;
fmax=20;
df=0.1;
totalscal=(fmax-fmin)/df;
f=fmin:df:fmax-df;%预期的频率
wcf=centfrq(wavename); %小波的中心频率
scal=fs*wcf./f;
%自己实现的小波函数
coefs2=cwt_cmor(z,1,3,f,fs);
figure(3)
pcolor(t,f,abs(coefs2));shading interp
%后面是函数
function coefs=cwt_cmor(z,Fb,Fc,f,fs)
%1 小波的归一信号准备
z=z(:)';%强行变成y向量,避免前面出错
L=length(z);
%2 计算尺度
scal=fs*Fc./f;
%3计算小波
shuaijian=0.001;%取小波衰减长度为0.1%
tlow2low=sqrt(Fb*log(1/shuaijian));%单边cmor衰减至0.1%时的时间长度,参照cmor的表达式
%3小波的积分函数
iter=10;%小波函数的区间划分精度
xWAV=linspace(-tlow2low,tlow2low,2^iter);
stepWAV = xWAV(2)-xWAV(1);
val_WAV=cumsum(cmorwavf(-tlow2low,tlow2low,2^iter,Fb,Fc))*stepWAV;
%卷积前准备
xWAV = xWAV-xWAV(1);
xMaxWAV = xWAV(end);
coefs = zeros(length(scal),L);%预初设coefs
%4小波与信号的卷积
for k = 1:length(scal) %一个scal一行
a_SIG = scal(k); %a是这一行的尺度函数
j = 1+floor((0:a_SIG*xMaxWAV)/(a_SIG*stepWAV));
%j的最大值为是确定的,尺度越大,划分的越密。相当于把一个小波拉伸的越长。
if length(j)==1 , j = [1 1]; end
waveinscal = fliplr(val_WAV(j));%把积分值扩展到j区间,然后左右颠倒。f为当下尺度的积分小波函数
%5 最重要的一步 wkeep1取diff(wconv1(ySIG,f))里长度为lenSIG的中间一段
%conv(ySIG,f)卷积。
coefs(k,:) = -sqrt(a_SIG)*wkeep1(diff(conv2(z,waveinscal, 'full')),L);
%
end
end
cwt的边缘效应与影响锥
由于小波计算中,小波系数是利用窗口函数和小波卷积而来的,当窗口在信号的边缘时,窗口内会存在一部分没有信号。这时,matlab就把窗口内这部分不完整的信号补零处理,凑够长度。
此时由于信号在边缘被强制补零,导致信号会失真,具体在时频图中表示为频率变宽,信号强度降低。严重的时候,甚至整个低频部分都会出现失真。这就是cwt的边缘效应。
为了确定边缘效应的影响,绘制出了一条影响曲线,曲线内部的信号影响小或者不受影响,曲线外部影响较大。曲线像一个锥形,高频处靠近两侧,低频处靠近中间,所以也被叫做影响锥。

所以根据边缘效应的原理,可以知道,之所以高频处影响范围小,是因为高频处小波被压缩,所以窗口更窄。低频处小波被拉伸,所以对应着窗口更宽。窗口的长度和小波的长度是相同的。
关于影响范围的评价,有很多种,这里为了方便说明,我直接用小波的半长度作为影响范围,来绘制影响锥。具体的思路如下,正常认为超过小波长度一半的范围都是失真的,然后通过频率求出每一点的小波长度,再在图上连线绘制出来。

引用
https://www.cnblogs.com/jfdwd/p/9249850.html
https://zhuanlan.zhihu.com/p/77072803
https://blog.csdn.net/weixin_42943114/article/details/89603208
自相关(Autocorrelation),也叫序列相关,是一个信号与其自身在不同时间点的互相关。非正式地来说,自相关是对同一信号在不同时间的两次观察,通过对比来评判两者的相似程度。自相关函数就是信号x(t)和它的时移信号x(t-τ)的乘积平均值。它是时移变量τ的函数。
公式为:

下面介绍一些信号的自相关函数说明应用:
- 自相关函数为偶函数, [公式] ,其图形对称于纵轴。因此,不论时移方向是导前还是滞后(τ为正或负),函数值不变;
- 当τ=0时,自相关函数具有最大值,且等于信号的均方值;
- 周期信号的自相关函数仍为同频率的周期信号;
- 若随机信号不含周期成分,当τ趋于无穷大时,自相关函数趋于信号平均值的平方。

自相关函数应用:
检测信号回声(反射)。若在宽带信号中存在着带时间延迟τ0的回声,那么该信号的自相关函数将在τ=τ0处也达到峰值(另一峰值在τ=0处),这样可根据τ0确定反射体的位置。
检测淹没在随机噪声中的周期信号。由于周期信号的自相关函数仍是周期性的,而随机噪声信号随着延迟增加,它的自相关函数将减到零。因此在一定延迟时间后,被干扰信号的自相关函数中就只保留了周期信号的信息,而排除了随机信号的干扰。 引用: https://zhuanlan.zhihu.com/p/77072803
在高速数据采样中,ADC时钟信号的稳定性对其性能有至关重要的影响,因为这些抖动会破坏高速ADC的时序。
孔径的定义

孔径时间ta,是指从采样时钟跳变开始,一直到保持电压建立。换言之,孔径是指采样保持电路中开关切换的时间,即从低阻态转换为高阻态的时间。由上面图可以看出,在ta时间内,模拟信号实际上是一直处于变化状态的,这就会导致量化值与实际模拟信号的一个延迟。对于一个确定的ADC来讲,孔径时间是一个定值。
孔径抖动

理想的时钟信号边沿应该是等间隔的,而上图所示的信号周期并不完全相同,这种情况成为时钟抖动。以此类推,孔径抖动,就是指ADC 孔径时间存在不确定性。在时间轴上,并不是完全的等间隔。

上图所示的ΔtRMS,即为孔径抖动。可以清楚看到ADC实际的采样时刻分散在TRACK+ΔtRMS时间内,TRACK为采样时钟,对应的电压变化范围是ΔVRMS.
其中
ΔVRMS = SLOPE * ΔtRMS
孔径时间和孔径抖动都是ADC的性能参数,是一个定值。

上图是一个高速ADC的孔径时间和孔径抖动。
采样时钟的影响
在上面的讨论中,ADC采样时钟TRACK是理想的,假设其抖动为ΔTRACKRMS.则有
ΔVRMS = SLOPE * ( ΔtRMS + ΔTRACKRMS)
由上式可以看出,电压不确定度和压摆率,采样时钟抖动成正相关。就是说,信号变化的越快,采样时钟抖动越大,则由此产生的噪声越大。
由下图可以明显的看出时钟抖动对于理想分辨率ADC的信噪比影响。在欠采样的情况下,会严重失真。
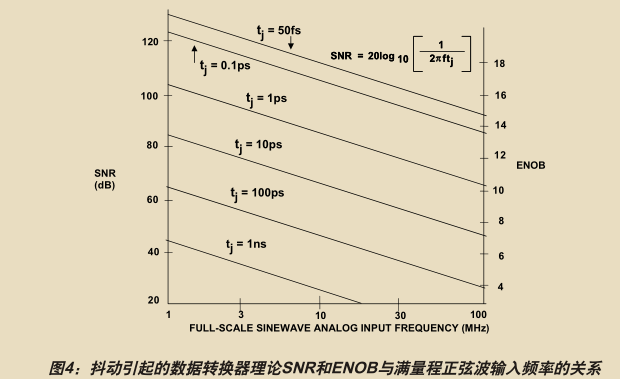
更完整的一个有关时钟抖动对SNR影响的公式如下图所示

抖动影响的时域分析
上面诸多论述,以频域分析居多,下面将更加直观分析时钟抖动造成的不确定性影响。
首先是采样过程,如图均匀采样频率Fs=,非均匀采样频率也是,但有较大噪声,两者都一共取点40个

到目前为止,采样过程并没有什么大问题,只是间隔出现了不一致。但是,请注意均匀采样的采样位置是可以确定的,即从零开始,落在N*1/20S 时刻;而非均匀的采样的采样时刻是不确定的。
下一步,信号还原。即以等间隔时间轴恢复采样数据。

上图蓝线是等间隔采样的恢复信号,橙色线是非均匀的时间采样的恢复,下图是非均匀采样的时间误差。
可以看到橙色线的信号出现了明显的畸变。如果采用更大采样速度,则可以看到明显的因为时间抖动而引入的噪声。

结论
ADC数据采样的恢复一定是按照已知的采样频率和采样间隔进行的,这就要求之前采样的时间间隔必须和恢复时间间隔保持一致,否则就会导致在A时刻恢复B时刻的情况出现。从而引入不确定性误差。这种误差会随着输入模拟信号频率的升高而进一步得到放大。
带限采样系统
传统的Nyquist带宽采样理论要求采样频率大于被采样信号频率2倍以上。

传统采样理论流程输入信号先经过低通滤波器,然后再进行逐点采样,最后形成离散的数字信号。
注意该低通滤波器的必须要滤掉原始信号中大于1/2采样频率的信号,以防止采样后出现频率混叠,干扰正常的采样信号。
还原过程就是DAC的过程,实际上我们只知道一个采样点和下个采样点的数值,我们并不知道两个采样点的具体大小,还原的过程涉及到内插,内插有很多种方法。

从工程角度上来说,目前ADC都由单独的芯片实现,我们在代码上获得的都是一个一个离散的点,还原数据,比如I2S转模拟音频,也都有专用的DAC芯片实现
传统奈穹斯特采样理论的难点在于采样时钟一单发生偏移的影响和采样还原(DAC)过程中使用sinc插值。因为采样定理要求的无线核插值sinc函数是非常困难的,一般情况下使用线性插值方法,效果如上图。
时钟偏移对采样的影响
信号的展开
假设a[n]是一个可数系数的集合,此系数决定于x。x[n]是一个确定信号集合,那么信号展开就是
$$x=\sum_{n}a[n]x_n$$
上面的式子就是说明原函数x就是和a[n],x[n]向量的线性组合。
信号采样实际上是将连续信号集合简化为一个可数的系数集合。
因此,没有任何先验信息,是无法以完整自由度角度去描述信号的。为了补偿信号空间上的损失,因此必须获得相关的结构。
比如 已知线性函数 x(t)= ax + b,还有已知x(0)和x(1),参数a和b是未知项目,那么对于t而言有
$$x(t)=x(0)(1 - t) + x(1)t=\sum_{0}^{1}a[n]x_n(t)$$
这里a[0] = x(0),a[1]=x(1),也就是说原始信号可以表示向量x_n和a[n]的线性组合。
但是,如果我们不知道x(t)的本身结构,就无法得到上面的式子。
从纯数学角度来说。不同于函数研究自变量和因变量之间的映射关系,这里将信号本身作为自变量来分析,这和泛函分析上的以函数作为自变量方法一致。因此涉及到一些集合,函数空间的相关知识。
$$x(t)=x(0)(1 - t) + x(1)t=\sum_{0}^{1}a[n]x_n(t)$$
回到这个式子,从线性代数的角度而言,如果x_n是线性无关的,或者说x_n组合成了一组基,那么代表了原信号是由向量集合{x_n}张成的空间。
超带限采样系统
超带限信号的采样不同于Nyquist采样,也称为欠Nyquist采样方法,突破2倍采样频率才能还原原信号的限制,来实现更低的采样频率采样原信号。该方法依赖输入信号本身的先验特征,信号处理方法根据不同任务开发不同算法结构。
经典的欠Nyquist采样包括
- 载波解调法。
- 带宽欠采样法。
FFT是一种用来计算DFT(离散傅里叶变换)和IDFT(离散傅里叶反变换)的一种快速算法。DFT的复杂度为O(n^2),而FFT的时间复杂度仅仅为O(nlogn)。
DFT的计算公式为:
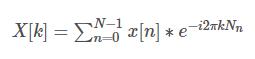
是针对离散的采样点 x[n]的傅里叶变换,其意义还是将信号从时域转换到频域。那么这里的 X[k] 表示的就是第k个点处的频域信号,下标k表示信号的频率, X[k] 的值就是该频率信号的幅值。这里可以看到,当k固定的时候,对应于频率为k的信号幅值是与 x[n]有关的一个级数的和,因此每一个频域的点实际上包含了所有时域点的信息。
有两点需要注意,一是因为 x[n]的长度为 N ,因此 DFT 后的频域信号 X[k] 的长度也是 N;二是由于算法计算的需要,N的取值一般是2的整数次幂。
将下标n分解为奇偶两部分,然后分别求和
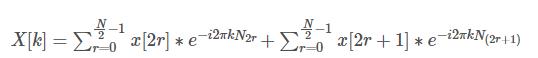
这里进行一次代换,用 x0[n]表示 x[n] 中的偶数项,用 x1[n] 表示 x[n] 中的奇数项
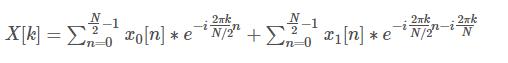
其中奇数项和偶数项的时间复杂度分别都是n^2 /4,也就是说总的时间复杂度是n^2 /2,也就是说相同的功能,使用后面那个计算方法,仅仅使用式子
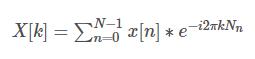
进行计算的一半运算次数,而两者得到的结果是一模一样的,但是这个时候N必须满足是2的整数倍。
如果奇数项和偶数项也是2的整数倍,是不是也可以再分为奇数项和偶数项,同时这个奇数项如果又是2的整数倍,也还能接着分,这也是为什么FFT输入数据一定要2的整次幂。
一个16个点的FFT运算,直观的看输入数据的变化,如下:

- 第一次将16个数据分为奇数和偶数,总共有2组
- 第二次四组
- 第三次8组
- 第四次16组

每进行一次操作,就能使得其中一半的计算量被减少。这样我们就把计算量从16^2,降低为2*log_2(16)。
引用
数字滤波器
滤波器根据实现方式可以分为经典滤波器和现代滤波器。
- 经典滤波器:假定输入信号中的有用成分和希望去除的成分各自占有不同的频带。如果信号和噪声的频谱相互重迭,经典滤波器无能为力。比如 FIR 和 IIR 滤波器等。
- 现代滤波器:从含有噪声的时间序列中估计出信号的某些特征或信号本身。现代滤波器将信号和噪声都视为随机信号。包括 Wiener Filter、Kalman Filter、线性预测器、自适应滤波器等
经典滤波器根据频率响应又可以分为:
- 低通滤波器(Lowpass filter) :通过低频,滤除高频。
- 高通滤波器(Highpass filter):通过高频,滤除低频。
- 带通滤波器(Bandpass filter):通过固定范围的频率。
- 带阻滤波器(Bandstop filter):滤除固定范围的频率。
以上 4 种滤波器的理想频率响应如下图所示:

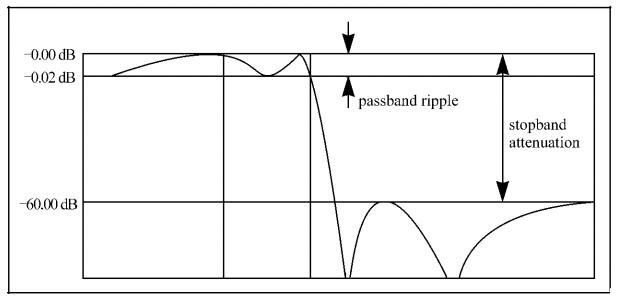
滤波器允许通过的频率范围为通频带,理想滤波器通频带的增益为1,所以信号的幅值不变。截止频带是滤波器不允许通过的频率范围。理论上滤波器在通带应有单位增益(0 dB),在阻带有0增益(-∞ dB),然而在实际中通阻带之间有一个过渡范围,如下图所示。在这一范围,增益在0~1之间。在应用中,允许增益在单位增益上下轻微变化,即允许有通带纹波。这一点也是实际滤波器与理想滤波器的区别。阻带衰减在实际中不是无限的,通带纹波与阻带衰减可表示为:

其中A0(f)、Ai(f)分别是一定频率f下的输出和输入振幅,通带波纹的单位为分贝(dB)。

例如对于-0.02dB的波纹:

这表明,输出和输入的幅值之比近似为1。
当阻带有-60dB的衰减,则

表明输出的幅度是输入的1/1000。
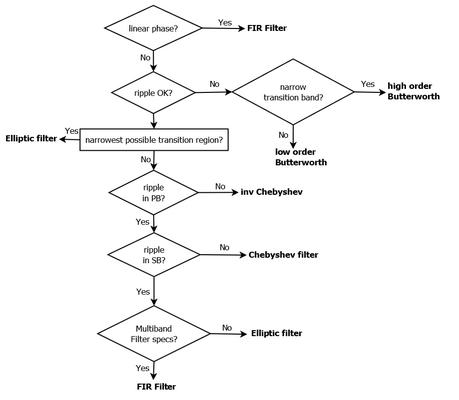
经典滤波器根据冲击响应的响应结果也可以进行分类:

的响应为冲击响应,如下图所示。由傅里叶变换后的频率响应可知滤波器在不同频率下的增益。理想情况下,通带增益为1,阻带增益为0;所以频率在通带范围内的信号可完全通过,在阻带的信号则不能通过。

如果冲击响应经一段时间后增益为零,则滤波器为有限冲击响应滤波器(FIR)或递归数字滤波器,反之则为无限冲击响应滤波器(IIR)或非递归数字滤波器。其最基本的不同是FIR的输出只是由当前以及过去的输入值决定;而IIR的输出不但由当前以及过去的输入值决定,还与过去的输出值有关。
一个FIR滤波器形如:

一个IIR滤波器形如:

IIR滤波器有较平坦的幅频特性,而且由于它的递归性,可以减少存储需求;
由于IIR设计方法源于传统的模拟滤波器,且使用滤波器时人们主要关心幅频特性,所以IIR滤波器使用较多。
数字信号处理中常见的IIR滤波器有:巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器、贝塞尔滤波器等,各个滤波器具有不同的频率特性。
FIR滤波器主要特点在于实现相位不失真,拥有非常好的相频特性,但是由于通常实现阶数较多,因此需要占用更大的存储空间。
相同参数的滤波器,IIR仅需要22阶,FIR需要100阶以上来实现:


对于数字滤波器的设计,设计之初就需要考虑如下问题:
- 是否需要线性相位;
- 通带是否允许纹波
- 窄带的过渡带
- 滤波计算的时间复杂度要求
在具体设计一种滤波器前,需对各种滤波器做多次试验
Z变换和差分方程
在连续系统中采用拉普拉斯变换求解微分方程,并直接定义了传递函数,成为研究系统的基本工具。在采样系统中,连续变量变成了离散量,将Laplace变换用于离散量中,就得到了Z变换。和拉氏变换一样,Z变换可用来求解差分方程,定义Z传递函数成为分析研究采样系统的基本工具。
对于一般常用的信号序列,可以直接查表找出其Z变换。相应地,也可由信号序列的Z变换查出原信号序列,从而使求取信号序列的Z变换较为简便易行。

Z变换有许多重要的性质和定理:
线性
设a,a1,a2为任意常数,连续时间函数f(t),f1(t),f2(t)的Z变换分别为F(z),F1(z),F2(z),则有:

滞后
设连续时间函数在t<0时,f(t)=0,且f(t)的Z变换为F(z),则有

数字滤波器的差分方程表示
数字滤波器的差分方程表示为:
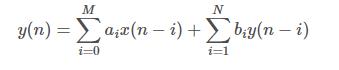
当N=0时候,表示的就是一个FIR滤波器,否则就是一个IIR滤波器。
可以用一个图来直观表示计算的过程:

上式进行z变换后得:

系统函数h(z)为:

其中ci为零点而di为极点。H(z)的设计就是要确定系数、或者零极点,以使滤波器满足给定的性能指标。
IIR滤波器的结构
数字滤波器的功能本质上是将一组输入数字序列通过一定的运算后转变为另一组输出数字序列。滤波器系统函数可以表达为多种不同的形式,每一种对应着不同的算法,也就对应着不同的实现结构。例如:

可以分解为:

或

上述同一系统的三种不同描述形式就对应了不同的实现结构,或者说不同的滤波器结构可以实现相同的传递函数。IIR滤波器常见的结构形式有直接Ⅰ型、直接Ⅱ型(典范型)、级联型、并联型。
通过差分方程能够画出包含反馈结构的数字网络称为直接型,对应的差分方程形式如:

计算结构图如下:

直接Ⅱ型将整个滤波器系统看成A、B两个子系统串联而成,由于为线性系统因此交换顺序不影响最终输出结果,传递函数可写为的形式如:
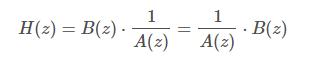
其差分方程是一个递归的形式如:

计算图如下:

同时还有:
- 并联型
- 级联型
对于IIR和FIR滤波器的设计,可以使用matlab的fdatools工具获得阶数和滤波器的结构以及对应的系数,然后就可以套入上面的公式进行滤波计算。
频域积分常用于加速度进行二次积分求位移的过程
时域中,加速度时程积分两次可以得到位移时程。在频域中,将加速度的傅里叶谱稍加调整后可以得到位移的傅里叶谱,然后反变换回来就是位移的时域谱。
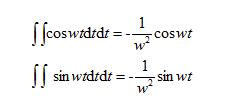

如果加速度经过滤波处理(主要是滤去高频成分,防止离散序列的频谱发生混叠),即便采样间隔很大,频域积分仍可以获得相当精确的结果,这种优势是时域积分难以比拟的。
数值积分结果误差大,究其原因,主要有两个方面。
第一,积分过程中受到“平移项”(直流偏置)的影响。可以通过简单的减去积分结果的均值来消除平移项的影响。国内外绝大部分测试软件中的数值积分都有此项功能。
第二,积分过程中受到“趋势项”的影响。
所谓趋势项是在测试信号中存在线性项或缓变的非线性项成分。工程实际测量的信号大部分是复杂周期信号与随机信号的混合,而且周期信号往往是研究对象。趋势项的存在会使数值积分的结果产生很大的误差,严重地背离真实情况。因此,在测试信号(积分求速度、位移时)中常要先消除趋势项,这是积分中的一个重要的中间步骤。
产生趋势项的原因主要有以下几种:
- 采样时未对原始信号进行适当处理,如高通滤波,使得信号中含有周期大于采样时间的极低频信号。
- 由于外界原因,包括传感器或仪器的零点漂移、基础运动等引起的信号波形偏移。
- 在截取记录时,样本长度选择不当。
- 由于操作不当,信号经过积分放大后产生趋势项,如零点未调准产生的常数,经积分后成为一条斜直线,低频噪声经积分放大后成为缓慢变化的趋势项。
转载
时域分析
时域特征值是衡量信号特征的重要指标,时域特征值通常分为有量纲参数与无量纲参数。
所谓“量纲”,简单地理解就是“单位”。有量纲的参数就是有单位的,比如平均值,一段温度信号(单位℃)的平均值依旧是℃;无量纲的参数没有单位,无量纲量常写作两个有量纲量之积或比,但其最终的纲量互相消除后会得出无量纲量,比如,应变是量度形变的量,定义为长度差与原先长度之比。
有量纲的特征值往往具有直观的物理含义,是最为常用的特征指标。有量纲特征值主要包括:最大值、最小值、峰峰值、均值、方差、标准差、均方值、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)、方根幅值等。
均值
均值是信号的平均,是一阶矩,可以表示为:
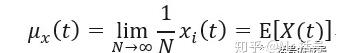
均方值
均方值是信号的平方的平均(信号→平方→平均值),代表了信号的能量,是二阶矩,可以表示为:

方差
方差是每个样本值与全体样本值的平均数之差的平方值的平均数,代表了信号能量的动态分量(均值的平方是静态分量),反应数据间的离散程度,是二阶中心距,可以表示为:
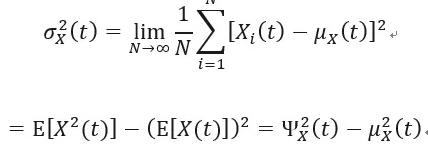
方差的不同表达方式,可以看出方差的几种理解方式:

式中可以看出:方差描述的是信号的离散程度,也就是变量离其期望值的距离。
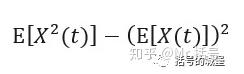
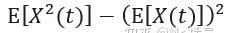
从物理含义上讲,均方值代表信号的能量,期望的平方代表信号的直流分量,而方差代表信号的交流分量。
标准差
标准差又叫均方差,是方差的算数平方根。标准差反应的是数据的离散程度。
方差和标准差都表示数据的离散程度,为了和原始信号统一量纲引入。
均方根
均方根(RMS)又叫有效值。将所有值平方求和,求其均值,再开平方,就得到均方根值。或者说均方根值等于均方值的算数平方根。

其物理含义可以这样理解:让交流电与直流电分别通过同一电阻,若两者在相同的时间内所消耗的电能相等(或产生的焦耳热相同),那么该直流电的数值就叫做交流电的有效值。
均方误差
均方误差(MSE)是某种意义上的方差,均方误差是指参数估计值与参数真值之差平方的数学期望值。如果我们把随机变量的数学期望E认为是参数估计值(未来的),把随机变量本身作为参数真值,那么均方误差就是普通方差。

均方误差MSE可以评价数据的变化(偏离)程度,MSE的值越小(相互之间的比较,而不是跟参数真值的比较),说明预测模型描述实验数据具有更好的精确度。
均方误差在机器学习中常作为一种误差量度。
均方根误差
均方根误差(RMSE)就是均方误差的算术平方根:

均方误差与均方根误差,正如方差与标准差一样,是量纲上的区别,应用不同场合。
总结

引用
正文
近年来现代信号处理学科高速发展。其中基于EMD(经验模式分解)的 Hilbert-Huang变换(HHT),由于能够分解出具有物理意义的分量,较之以往只能在数学框架内实现分解的信号处理方式,是一种本质性的飞跃,因此现在在很多领域都得到了很好的应用。
希尔伯特黄变换是1998年由NordenEHuang等人提出的一种信号分析方法。它是一种能够有效分析线性/非线性,平稳/非平稳信号的时频分析方法。它的核心是经验模态分解(简称EMD)和希尔伯特变换(简称HT),前者是信号分解(或者信号变换)方法,后者是信号分析(谱分析)方法[l]。考虑到信号分析理论的完整性和不同分析方法之间的差异,对傅立叶变换、小波变换理论和WVD分布等信号分析方法也作了简单的介绍。
传统的傅立叶频谱分析方法将信号表示从时间空间变换到频率空间,能够表示信号全局的能量一频率分布。因此,通常谈论到频谱特征,总是习惯的和信号的傅立叶变换联系在一起。然而应用傅立叶变换必须注意到一些严格限制的条件:系统必须是线性的;数据必须满足周期性或者是广义平稳的;否则,用傅立叶变换分析这样的信号就无法得到具有实际物理意义的结果。
Noulen E Huang在他的论文中提到[1]不论来自物理测量还是数学模型所得到的信号,都有可能面临下列一个或几个问题:
- 总的信号长度太短;
- 信号是非平稳的;
- 信号代表着非线性过程。
其中上面的前两个问题是相关的,如果信号的长度比平稳过程的最大时间区间(或者说最大时间长度)小的话,将表现出非平稳性,而在自然界,我们面临的大部分现象都是短暂的,所以非平稳性是普遍存在的。此外,由于传感器、量化等非线性因素,实验中得到的数据极有可能是非线性的。
到了近代,所研究的信号更普遍,更贴近实际生活:比如像心音信号,语音信号,地震信号,机械振动信号,图像信号,那么采用非平稳随机信号模型将更加合理。为了对这类非线性非平稳信号进行有效的分析和处理,相继诞生了不同的时频分析方法。
希尔伯特变换与瞬时频率
传统的傅里叶分析用一系列三角基函数对信号进行正交运算,但是对于非平稳信号,比如频率一直变化的信号,得到的傅里叶谱只是某一段时间内频率的均值,无法准确描述频率-时间的变化。
瞬时频率的定义方法不唯一,但使用Hilbert变换来定义瞬时频率能够生成复解析信号,进而得到复平面上具有明确解析意义的瞬时频率。对于实信号x(t),其复解析信号为

对实部虚部的幅角对时间求导即得到瞬时频率。
瞬时频率
 应当是关于时间t的单值函数,即所谓频率上的单分量函数,联想一下传统傅里叶变换中“时域信号是多个三角基函数之和组成”的概念,这就是最大的区别。
应当是关于时间t的单值函数,即所谓频率上的单分量函数,联想一下传统傅里叶变换中“时域信号是多个三角基函数之和组成”的概念,这就是最大的区别。
经验模式分解
要求得信号的瞬时频率,必须将信号分解为瞬时频率有物理意义的分量,这就是EMD的目的。黄锷提出了IMF的概念,关于IMF需要满足哪些条件相信教材上已经讲的很清楚了。由于使用样条曲线及其中值进行多次的分解运算,每次分解后时间序列点的密度就对半减少、同时时域上的幅值也对半减小,因此EMD也实现了时域和频域上的多尺度分解,类比一下小波就能发现EMD的这个特点。
Hilbert谱与Fourie谱
对每个IMF进行Hilbert变换,原信号x(t)可以表示如下,即Hilbert谱

对比一下Fourier谱
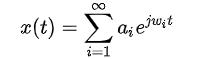
比较一下ai和wi,可以发现Hilbert谱是Fourier谱的推广,更具一般化意义,因此才有了上面所说“傅里叶变换得到的频谱其实只是某段时间内频率的加权后均值”。
引用
[信号处理的功率谱](https://www.jianshu.com/p/b3e867e73473)
基本概念


功率谱和功率谱密度是不同的。若能量为E,时间为T,频带为F,则功率谱是表示为E/T;而功率谱密度是表示为E/T/F。所以它们的量纲和单位是不同的,表示了不同的物理量。但又由有常把功率谱当作功率谱密度的简称,所以经常容照耀混淆。
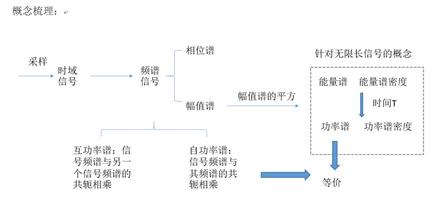
为什么要用功率谱估计
对于随机信号描述平均功率才有意义——如何描述平均功率
信号按照是否可以用确定的时间函数/图表来表达可以分为:
- 确定信号
- 随机信号
同时按照能量和功率是否有限又可以分为:
- 能量信号(能量有限,平均功率为0)
- 功率信号(能量无限,平均功率有限)
- 非功率非能量信号


若信号的总能量是有限的,可以用能量谱或幅值谱来考察。能量信号的能量是一个非无穷的正值,这时候就可以把能量作为考察能量信号的有效量纲,而且由于能量信号的能量有限,能量信号的平均功率肯定是无限接近于0的,这时候从平均功率的角度去考察能量信号就没有意义。
若信号的总能量是无限的,但单位时间内的能量是有限的,则用功率谱密度函数考察。功率信号的能量是无穷的,从能量角度去考察就没有意义了,但是功率信号的平均功率肯定是个非零值,这时候选择平均功率作为考察的量纲就是合理的。(信号做功消耗能量,平均功率是信号所做的功与无穷时间的比值。)
一般地,若信号的总能量是有限的,用能量谱密度函数考察;若信号的总能量是无限的,但单位时间内的能量是有限的:比如周期信号,用功率谱密度函数考察[4]。
一般我们将对能量信号的分析称为能量谱分析,对功率信号的分析称为功率谱分析
为什么要引入能量信号和功率信号的概念,为什么不用幅值谱:
对于随机信号而言,它的频谱是不存在的,也就是说不能用频谱来表示这个信号,所以这是一个典型的功率信号表示问题(因为随机信号在时间上是无限的,在样本上也是无穷多,因此随机信号的能量是无限的,随机信号一定是功率信号)。
(可以这么理解:如果取截断来看,随机信号的频谱是一直在变化的,所以对于一个无限长的随机信号而言,它没有可以表示的频谱。以上的话说的正式一点,就是:
功率信号不满足付里叶变换的绝对可积的条件(即狄里赫利条件,保证积分是收敛的,而不是无穷大),因此其傅里叶变换是不存在的。)
对于周期信号:
周期信号有的是能量信号,有的是功率信号,对于周期性信号中的功率信号,同样不能使用频谱分析。
所以根据狄里赫利条件,能量信号可以直接进行傅里叶变换,而功率信号不行。对于无法做傅里叶变换的信号,只能走一步弯路,先求自相关,再做傅里叶变换。但是物理意义上就是功率谱了。
一个信号有三个组成部分:幅值、相位和频率成分。对于随机信号而言,这三个组成部分都是随机的,当然它的幅值是围绕平均值在交变,包含所有的频率成分,相位完全杂乱无序。任一时刻与下一时刻之间没有任何关联,所以,不能用确定的数学函数来表征,只能从统计学角度来分析处理。(如果硬要截断后做fft,也可以,只不过没有确定的意义)。
功率谱分析是统计学意义上的对信号的表征
一个信号有三个组成部分:幅值、相位和频率成分。对于随机信号而言,这三个组成部分都是随机的,当然它的幅值是围绕平均值在交变,包含所有的频率成分,相位完全杂乱无序。任一时刻与下一时刻之间没有任何关联,所以,不能用确定的数学函数来表征,只能从统计学角度来分析处理。
在一定条件下,各种随意形状概率分布生成的随机变量,它们加在一起的总效应,是符合正态分布的(中心极限定理)。

(上式也可以这么理解:均值表示信号中直流分量的大小,方差表示信号交流分量的平均功率,均方差表示信号的平均功率,所以:信号的平均功率= 信号的直流功率+ 信号的交流功率)
平稳随机信号是趋于正态分布的(所谓的平稳是指分布参数不随着时间的变化而变化),决定正态分布的两个参数:
- 平均值u:基本为0,不为0时,一般也会移除直流量使其为0
- 方差:当均值为0时,那么唯一能够表征随机信号的就是方差
而此时,均方差和方差是相等的,又因为均方差表示的信号的平均能量,所以对于平稳随机信号而言,描述平均功率才有意义。
(对于非平稳信号,一般的处理方法是找一个时间窗,认为它在这个时间窗内是平稳的)
如何计算功率谱

- 直接法 时域信号进行傅立叶变换,得到频域分内,然后平方积分即可以得到功率谱密度,理论上随机信号直接做FFT的做法其实就是截断成能量信号进行处理,这种处理不符合随机信号定义,但之所以这样做,是做短时频域分析下作的近似处理
- 自相关法
从理论上来说,功率谱是信号自相关函数的傅里叶变换。因为功率信号不满足傅里叶变换的条件,其频谱通常不存在,维纳-辛钦定理证明了自相关函数和傅里叶变换之间对应关系。

参考资料
参考资料 [1]https://zhuanlan.zhihu.com/p/22513006 各种谱函数的区别是什么,何时用何种函数?
[3] https://zhuanlan.zhihu.com/p/40481049 如何理解随机振动的功率谱密度?
[4]https://www.zhihu.com/question/39592966/answer/875419230 如何理解功率信号和能量信号
[5] https://zhuanlan.zhihu.com/p/22571798 谱线是怎样影响随机信号和周期信号的PSD或自谱的
[6]https://blog.csdn.net/fengzhuqiaoqiu/article/details/101153157 能量信号和功率信号的分别
[7]https://www.cnblogs.com/l20902/p/10610962.html 能量谱密度功率谱密度
[8] https://my.oschina.net/wangsifangyuan/blog/875891 功率谱和频谱的区别、联系
[9]https://blog.csdn.net/FPGADesigner/article/details/88532027 MATLAB数字信号处理(1)四种经典功率谱估计方法比较
[10]https://zhuanlan.zhihu.com/p/143545782 数字信号处理:功率谱估计的对比分析
[11]https://blog.csdn.net/dujiahei/article/details/80233999 功率谱密度函数估计
[12]《概率论与数理统计》第四版——第十四章平稳随机过程
[13] https://www.zhihu.com/question/68698069/answer/275980099 为什么随机信号不能用频谱表示?而必须用功率谱、密度表示呢?
[14] https://wenku.baidu.com/view/7703fc5f951ea76e58fafab069dc5022abea46f0.html?fr=search matlab实现功率谱密度分析psd及详细解说
引用
https://zhuanlan.zhihu.com/p/166342719
Kalman Filter既是控制设计方面学习者的需知常识,也是传感器系统设计和优化,信号处理,系统辨识等领域的实践者的必备知识。理解Kalman filter需要大概四块领域的知识:
- 概率和随机过程理论(Probability and Random Process Theory)
- 统计学和最优估计理论(Statistics and optimal estimation)
- 信号处理 (Signal Proccessing)
- 动力学系统常识(Dynamic Systems)
什么是卡尔曼滤波
卡尔曼滤波器和它的用途
Kalman filter这个名字是以控制领域大神R. E. Kalman命名的一种滤波技术,或者说状态估计(state estimation)方法。如果不以他名字来命名,这个方法还可以叫做Linear Least-Mean-Squares Estimator(线性最小均方差估计),或者Linear Quadratic Estimator (线性二次型估计)[1,p1]。Kalman Filter的使用对象通常是一个线性随机系统(Linear stochastic system),通过测量的含有随机噪音的输出来估计出最优的系统状态。这种最优性是建立在使得mean squared errors(MSE)最小的意义下,故有这两个名字。你可能还听说过Extended Kalman filter(EKF,扩展卡尔曼滤波器),Adaptive Kalman Filtering(AKF, 自适应卡尔曼滤波)等等名词,先别着急,在把基本的知识介绍完后,再看也不迟。更多关于Kalman的一些事迹,将来有机会专门读些资料作为科普写一写。
Kalman filter的应用十分广泛,提供了可以真正实用的针对有限维随机系统的实时状态最优估计。它作为一种工具,主要有两方面的应用:state estimation 与performance analysis of estimation system[1,p4]。
状态估计(state estimation)
我们之前讲过用Luenberger observer来估计线性时不变系统(LTI)的状态,那时候我们并没有考虑系统的输出中夹杂着的随机噪音的信息。注意!如果你看过我这个专栏之前关于观测器的文章,Luenberger observer是通过反馈的手段来抑制最后输出中的不确定性。我们知道在Luenberger observer的观测器方程中存在一个增益矩阵 [公式] ,与之相乘的是观测器输出与系统实际输出的差值。在Luenberger observer方程推导中我们并没有显示地去考虑噪音给我们带来的问题,而是把噪音的麻烦“下意识”地交给了反馈。采用反馈的目的就是抑制不确定性,那么噪音可以视为扰动,也就相对地会被这样的反馈设计所抑制。Kalman filter也干的同一件事:状态估计。因此Kalman filter也是一种observer。Kalman filter具有非常类似的结构,有预测值和实际观测值的参与去不断更新所谓的filter gain。filter gain是随着观测进行不断迭代而改变的,并不像Luenberger observer中的矩阵 [公式] 往往是一个固定值。它们在噪音方面处理的主要不同是,Kalman filter的建模将noise的统计学信息作为已知信息考虑到了gain的设计中,而Luenberger observer却没有考虑噪音的任何信息。往往Luenberger observer的设计希望矩阵 [公式] 都是相对准确的以达到最好的估计效果,而实际情况往往不如人愿。Kalman filter考虑了系的动态过程中存在的随机性,更好地利用信息去完成系统状态的估计。
估计系统的性能分析(performance analysis of estimation system)
Kalman filter可以参数化表征其估计误差的大小,从而便于我们清楚是哪一个系统参数影响了最后的估计误差结果,这是有利于设计者分析估计系统的性能和提高估计精度的重要性质。比如采用的传感器种类,传感器位置,传感器带宽,噪音分布等等,都可以作为估计误差函数的参数。这种性质就可以帮助我们去做各个因素之间的权衡,指导我们去优化系统性能,而不是跟无头苍蝇一样trial and error。
为什么称之为 “滤波器”
这是许多信号处理和控制的初学者经常问的一个问题:文献和书上总是出现filter或者filtering这个词的含义是什么?包括在computer science领域的imagine processing领域,我们也时常能看到各种滤波算法。
filter,原来的意思就是过滤器,或者俗称筛子。所谓过滤器,我们都知道,学化学或者生物的时候我们用来去处混合物中的杂质(impurities)用的。包括现在的很多净化产品,比如自来水过滤头,空气净化器本质上起到了的就是过滤作用。后来filter这个词被引入了信号处理领域,所谓的impurities在这个领域中往往是我们不想要的噪音(noise)分量。我们听过的低通滤波器(low-pass filter),高通滤波器(high-pass filter),带通滤波器(band-pass filter),无论是数字的还是模拟的,都起到了滤除信号中不想要频率的作用。我在之前的专栏文章中也讲过,一个实际系统频响幅值越往高频走越小,信号输入系统后,其输出相当于通过了一个low-pass filter,此时该系统也可以被称为一个滤波器。这类对filter的理解,是“改变”了输入信号的频域信息,使得对应输出达到了我们想要的去除噪音的效果。 把噪音和filter的定义广义化,我们可以定义不同物理形式的滤波器。
不同于关注点在频率设计上的滤波器,Kalman filter和维纳滤波器(Wiener filter)采用了噪音和系统状态的统计学信息,一般以最小化mean-squared error(均方差)为优化目标,来给出原输入信号的最优估计(optimal estimation),这个estimation的最优性(optimality)是以最小均方差为准的。Kalman filter和Wiener filter之间有各方面的差别,我们这里暂时不去细究。从实际应用上来讲,Kalman filter和它的改进版本由于适用于nonstationary process(非平稳过程)使用更加广泛。既然能够以某种最优标准还原信号,Kalman filter就拥有了一个与filter等同的功能:降噪(noise reduction)。这也是为什么Kalman filter被称之为所谓的滤波器的原因。
我们回过头来说,filter就是一类能够实现filtering的device或者algorithm。那么filtering又如何定义?[2,p10] 我们可以从两个方面去理解:
- 使用可测量的信号,还原不能被直接测量或者带有噪音的信号。
- 区别另外两种不同的信号处理方式:smoothing 和 prediciton
所谓的estimation就包含三种处理信号的方法:filtering(滤波),smoothing(平滑) 和 prediciton(预测)。在第二个层面的理解中,我们把filtering理解为:根据到目前时间 [公式] 为止的信号的所有信息,来还原信号的部分或者全部信息。
Smoothing,所谓的信号平滑,并不要求只使用当前时间 [公式] 之前的信息来估计真实信号,而是可以采用t之后的一段时间内的测量信号,返回来估计时间 [公式] 的信号。简单说,我拥有了一段10秒长的信号,用10秒的信息回过头来过去信号在第5秒的值。这说明smoothing的估计并不是即时的,而是有一定的延迟(第5秒的信号估计,却延迟了5秒,等第10秒的信息得到后再得出。)。Smoothing是一块单独可以拿出来讲的内容,在这一系列中就不多做展开了。可想而知由于smoothing用到了更多的信息,理论上估计精度应该会更好。
Prediciton,信号预测就不用多说了吧? 现在最火热的行业和研究领域莫过于AI了,其中的机器学习也好,深度学习也好,目标说到底是通过训练,代替人去做更好的预测。一般prediciton用到的信息就是截止到当前为止,然后输出是对未来的估计。

随机变量(Random Variable)
概率的基础定义我就跳过了,多数人都可以通过简单定义理解。我们来说说随机变量(random variable)和随机过程(random process)的一些内容。随机变量X是一个定义在样本空间上的实值函数,把样本点映射成一个实数。每个样本点都有不同的概率出现,意味着随机变量的取值也是随机的,并且服从某个分布(distribution)。一个随机变量X的distribution是由 累积分布函数(cumulative distribution function,CDF),或者简称distribution function来刻画的,是以一个实数为自变量的函数:

对于连续取值的随机变量,distribution function可以由概率密度函数(probability density functioin,PDF),p(x)来表示:

他们两个之间的积分关系应该很容易理解。那么对于多个随机变量,我们可以定义联合积累分布函数(joint cumulative distribution function):
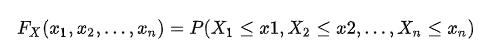
其联合概率密度函数(joint probability density function) :
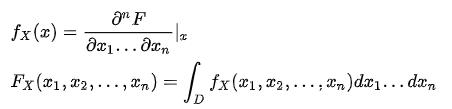
对于多元随机变量的情况,我们还可以定义marginal distribution function和marginal probability density function, 当我们只考虑其中一个随机变量时的分布时。
我们讲讲distribution的统计特性。随机变量最重要和常见的两个statistical measure就是数学期望(expected value)和方差(variance)。我们只说连续随机变量。一个随机变量的期望或者说均值(mean)的定义为:

其中 p(x) 是 x 的概率密度函数。要指出的是,我们还经常把(5)叫做distribution的期望或者均值,所以这两种说法是一回事。E(X) 是随机变量或者分布的所有可能取值的概率加权,X 的取值理应在这个E(X) 附近波动。而描述数据的波动性,我们采用方差,其定义如下:

之所以有(6)化简的结果,还要利用 ,因为理论上 E(X) 是确定的。如果我们有一个随机变量的函数 g(x) , 那我们也可以定义上述期望和方差。我们也时常用
,因为理论上 E(X) 是确定的。如果我们有一个随机变量的函数 g(x) , 那我们也可以定义上述期望和方差。我们也时常用 来表示expected value和variance。
来表示expected value和variance。
一个随便变量X或者随机变量对应分布的矩(moment)是由如下积分定义的:

上式称之为随机变量X关于实数c的k阶矩(The k-th moment of random variable X or distribution about a value c)。当 c = 0 时,我们将结果称之为raw moment(原点矩),当  时为中心矩(central moment)。矩的定义跟物理中的moment的定义是相同含义的,即表示物理量与对应距离乘积的积分,最常见的就是力矩了。矩就是一种综合考量了距离和量大小的量。根据(7),我们发现所谓期望就是一个随机变量的first raw moment, 方差就是 X 或者对应distribution的second central moment。second raw moment是X的mean squared value:
时为中心矩(central moment)。矩的定义跟物理中的moment的定义是相同含义的,即表示物理量与对应距离乘积的积分,最常见的就是力矩了。矩就是一种综合考量了距离和量大小的量。根据(7),我们发现所谓期望就是一个随机变量的first raw moment, 方差就是 X 或者对应distribution的second central moment。second raw moment是X的mean squared value:

定义root mean square(均方根,RMS)是:

一个随机变量的标准差(standard deviation) 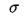 被定义为方差的平方根,标准差的引入使得其值得量纲与均值是一致的,便于分析。一个随机变量的rms是其标准差,如果 E(X) = 0 。数学期望和方差实用的性质:
被定义为方差的平方根,标准差的引入使得其值得量纲与均值是一致的,便于分析。一个随机变量的rms是其标准差,如果 E(X) = 0 。数学期望和方差实用的性质:

协方差(covariance)是刻画二维随机变量 Z=(X,Y) 的两个分量之间相关性的一个特征数,由两个变量与其期望差值的乘积的期望定义:

当协方差大于0,则正相关,表示两个偏差同时增加或减少,反之则反方向变化。如果为0,则表示两个变量不相关,有可能是毫无联系,也有可能存在非线性关系。不相关(uncorrelated)和独立(independent)是两个概念,不相关比独立要更弱一些。如果两个变量是独立的,那么它们也是不相关的,则  。反之,却不一定成立。所以成立的条件可以弱化为X,Y不相关即可。
由协方差的定义我们可以计算:

为了消除协方差的量纲,引入取值在-1到1之间的(线性)相关系数(correlation coefficient):
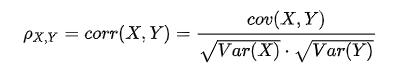
如果用向量和矩阵的形式来写 n 维随机向量的期望:

用协方差矩阵(covariance matrix)来记录随机变量各分量的协方差:

对角线上的协方差其实就是各分项的方差 Var(x_i) 。Covariance matrix有许多重要的应用,它是一个对称的,非负定矩阵(nonnegative definite matrix).
Random Process 随机过程
随机过程(Random process)是一个时间序列。它可以看成是一个随机变量簇  ,在每一个时刻 y , 都有一个独立存在于此时刻的随机变量X_t及其分布。在单独的某个时刻,它与之前讨论的随机变量无异。所以有无数个随机变量在相应的时间处取值,然后构成随机过程X(t)。
,在每一个时刻 y , 都有一个独立存在于此时刻的随机变量X_t及其分布。在单独的某个时刻,它与之前讨论的随机变量无异。所以有无数个随机变量在相应的时间处取值,然后构成随机过程X(t)。
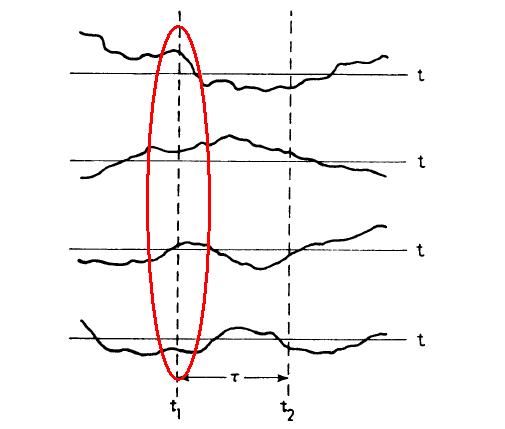
我们也可以认为随机过程  是无数个时间函数的集合,随机过程的一个具体实现 X(t) 就来自这个时间函数的集合。一个一般的随机过程在每一个时刻 t 的分布函数是一个时变函数:
是无数个时间函数的集合,随机过程的一个具体实现 X(t) 就来自这个时间函数的集合。一个一般的随机过程在每一个时刻 t 的分布函数是一个时变函数:

概率密度函数为:

同样的可以定义二阶联合概率分布函数和密度函数表示两个时间点 t=t1,t=t2处联合概率。一般随机过程的统计特征是随着时间而改变的:

有一类随机过程是很特殊的,对于任意选取的n个时间点tn ,和一个任意延时 τ,都有n阶联合概率密度函数:

则称随机过程  是stationary(平稳的),或者strictly stationary。由于任意一段时间 τ 内的联合概率密度函数不变,这意味着随机过程的各项统计特性都是保持不变的(前提是存在,可能有期望和方差都不存在的情况,比如满足柯西分布的平稳过程)。实际上这种假设只是理想的,按定义是难以验证的,实际中一般只能近似,严格说所有自然随机过程都是非平稳的(non-stationary)。工程中常见的是weak or wide-sense stationarity(WSS,弱平稳过程,或宽平稳过程)。所谓WSS random process,是指二阶矩
是stationary(平稳的),或者strictly stationary。由于任意一段时间 τ 内的联合概率密度函数不变,这意味着随机过程的各项统计特性都是保持不变的(前提是存在,可能有期望和方差都不存在的情况,比如满足柯西分布的平稳过程)。实际上这种假设只是理想的,按定义是难以验证的,实际中一般只能近似,严格说所有自然随机过程都是非平稳的(non-stationary)。工程中常见的是weak or wide-sense stationarity(WSS,弱平稳过程,或宽平稳过程)。所谓WSS random process,是指二阶矩  存在,均值是常数,且自相关函数(autocorrelation)仅与一个时间差 τ相关的随机过程。
一个实值随机过程的自相关函数(autocorrelation function, ACF)是由下式定义的:
存在,均值是常数,且自相关函数(autocorrelation)仅与一个时间差 τ相关的随机过程。
一个实值随机过程的自相关函数(autocorrelation function, ACF)是由下式定义的:
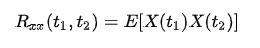
对于WSS RP我们有autocorrelation:
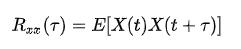
同理也可以定义auto-covariance function以及两个随机过程之间的cross-correlation.
让我们考虑WSS的具体均值和自相关函数的计算。一般获得WSS的统计特性,需要重复多次试验,得到多条随机过程的实现 $$X_i(t)$$,然后根据试验次数来求样本均值或者样本自相关值来近似真实值。
但是重复增加试验次数,并不是一个好办法,我们就想如果只通过一个试验样本,但是加长时间,是否也能准确地去计算其统计特性。
各态历经假说(ergodic hypothesis)指的就是一个宽平稳随机过程的统计特性,通过其全部可能的实现 $$X_i(t)$$ 的平均统计特性值计算的结果,与任意一个实现$$X_p(t)$$在全部时间上求平均值得到的结果,是一样的。实际中几乎所有的宽平稳过程的统计特性都是基于ergodic hypothesis,通过一个试验结果来计算的。
这里注意,我们讲宽平稳过程,而不是严平稳过程。对于一个严平稳过程,很难实际验证,并且其期望和方差都不一定存在,也就无所谓通过求时间均值的办法来逼近了。
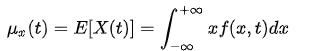
计算均值的方法是一种理论上可以计算WSS均值的办法,这是将每一个时刻的随机变量与其概率相乘再积分的办法;我们还可以理解一个随机过程 所有可能实现的集合,所以均值也就是同一个时间段内的不同可能实现的 X(t)的时间均值,我们可以根据下式来计算其均值:
所有可能实现的集合,所以均值也就是同一个时间段内的不同可能实现的 X(t)的时间均值,我们可以根据下式来计算其均值:

当然只是理论上的,一方面同一个时间段理论上只能得知一个实现$$X_p(t)$$(不可能时间倒流回去再得到同一段时间内的另外一个实现),另一方面实现的数量也只能是有限的。实际操作中,实际只能取有限个试验序列来近似。ergodic hypothesis告诉我们均值也可以通过时间均值来计算:

即同一个试验序列的均值只要时间够久也能收敛到  。其他的统计特性同理,比如WSS的自相关函数我们可以根据下式计算:
。其他的统计特性同理,比如WSS的自相关函数我们可以根据下式计算:
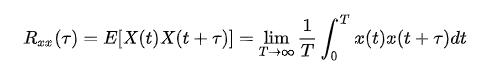
信号处理理论
接触过信号处理的话,你上来可能就听说过两个词: 功率信号(power signal)和能量信号(energy signal)。上来我们可以直接把这两个词的定义给背一遍:
- energy signal就是指信号具有有限的能量,在无穷时间中其平均功率为0。
- power signal是功率有限的信号,在无穷时间中的积累表明其具有无限的能量。
要理解上述定义,我们首先定义signal processing中信号的能量(energy):

这与物理学中的能量并不一样,但是却有联系。如果是电压信号,那么上式计算的能量量纲是  ,而电路理论中能量的单位是  。
有了能量的概念,我们可以顺势定义一个信号的功率,大概想想是能量与时间的比值。问题是上式E中定义的能量是在无穷时域中定义的,这时候我们要问,是否有些信号的能量根据E计算是有限的,或者是无限的。如果根据E我们发现一个信号在无穷时域中的  ,那么这个信号就是energy signal。对于一个连续时域信号,在无穷时间内的平均功率为:

对于energy signal,显然无穷时间内的平均功率为0。那么如果一个信号的能量理论上是无限的,E的分子是无穷的,分母也趋向于无穷,最后平均功率又会什么呢?如果分子的发散速度比分母快,那么其平均功率会无穷大时;如果分母发散更快,则平均功率为0;如果发散速度在无穷时域内基本都能保持的差不多,最后平均功率会有界。如果一个信号在无穷时域上的能量理论上是无穷的,并且其平均功率是有限的,我们就称这个为功率信号power signal。问题来了,哪些信号是功率信号呢?
周期信号是功率信号。假设时间为 T=nT0 , T0 是周期信号的周期,那么平均功率P就成为了:

现实中的周期信号,在周期区间上分母都是有界的,很明显P最后的结果一定是有界的,所以一般周期信号是功率信号无误。
宽平稳随机信号也是功率信号。一般的随机信号是不一定满足能量无限且 有界的。我们这里考虑满足各态历经假说的宽平稳随机信号。如前所述,它的统计量是可以通过单一信号在无穷时域中的平均值来逼近的,如同
有界的。我们这里考虑满足各态历经假说的宽平稳随机信号。如前所述,它的统计量是可以通过单一信号在无穷时域中的平均值来逼近的,如同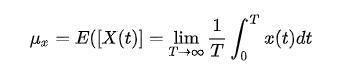 的WSS process那样。在各态历经假说成立的情况下,我们知道宽平稳随机信号的二阶矩
的WSS process那样。在各态历经假说成立的情况下,我们知道宽平稳随机信号的二阶矩  存在,均值为常数,并且可以通过时间均值来计算:
存在,均值为常数,并且可以通过时间均值来计算:

由于μ是一个常值,所以我们可以断定 E[(X(t)^2] 是有界的,我们把这个一个信号的 E[(X(t)^2] 叫做均方值(mean squared value)。一般宽平稳随机信号满足ergodic hypothesis,我们就有均方值:
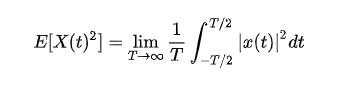
很明显这就是平均功率的定义,所以我们说此满足WSS过程定义的信号是一个功率信号。而均方值的平方根,正是RMS,工程上常称之为有效值(算交流电的有效值时我们碰到过这个概念)。如果WSS信号均值为0,那么信号的平均功率根据就是其方差。
我们关注功率信号,因为我们通常把采集到的随机信号认为是功率信号。根据帕塞瓦尔定理(Parseval theorem),时域信号的能量与频域内该信号的能量相等:

对于能量信号,我们可以定义  为能量谱密度(energy power density)来描述信号能量在各频率上的分布。对于功率信号,我们要采用功率谱密度(power spectral density, PSD),或者自功率谱、自谱,来描述其平均功率的在频域上的分布。我们把平均功率转换到频域中:
为能量谱密度(energy power density)来描述信号能量在各频率上的分布。对于功率信号,我们要采用功率谱密度(power spectral density, PSD),或者自功率谱、自谱,来描述其平均功率的在频域上的分布。我们把平均功率转换到频域中:

这里的  就是自谱。至于说到底频率的单位是Hertz还是radian,这个看单位,并不关键。随机过程有很多个可能的实现,它的统计平均功率谱密度是
就是自谱。至于说到底频率的单位是Hertz还是radian,这个看单位,并不关键。随机过程有很多个可能的实现,它的统计平均功率谱密度是 。根据Wiener–Khinchin theorem, 我们知道宽平稳随机过程的PSD与其自相关函数是互为傅里叶变换的:
。根据Wiener–Khinchin theorem, 我们知道宽平稳随机过程的PSD与其自相关函数是互为傅里叶变换的:

实际中自相关函数是可以获取的,所以可以通过这层关系来估算WSS过程的自谱。实际中PSD只能通过一段截短的信号来估算,在MATLAB中有一些函数可以提供估算结果,叫periodogram,有专门的算法。最常见的估计PSD的方法是Welch's method,见MATLAB参考。以下是一点额外的参考资料:
如何理解随机振动的功率谱密度?
能量信号、功率信号、频谱、能量谱、功率谱、及一些定理
白噪声(white noise)一种理想的随机信号,其功率谱在所有频率中是一个非零常数。如果功率谱不是一个常值,却也在全频率分布,被认为是噪声的信号,我们称之为有色噪音(colored noise)。白噪音是 power spectral density定义为常数:
power spectral density定义为常数:
由于自相关函数的Fourier变换是功率谱密度函数,所以我们知道白噪音的autocorrelation function [公式] 为:

其中  是Dirac函数。因为Dirac函数在原点处无穷大,我们就知道白噪声的幅值只有当τ = 0 )时才与自身相关,而其他任何时候各时刻幅值均不相关。由于功率谱无限宽,其带宽也是无限宽的,现实中无法实现,但是现实中常会把一些信号近似为白噪声去研究。所谓“白”色,也是由于白光含有所有频率的不同单色光得名。
是Dirac函数。因为Dirac函数在原点处无穷大,我们就知道白噪声的幅值只有当τ = 0 )时才与自身相关,而其他任何时候各时刻幅值均不相关。由于功率谱无限宽,其带宽也是无限宽的,现实中无法实现,但是现实中常会把一些信号近似为白噪声去研究。所谓“白”色,也是由于白光含有所有频率的不同单色光得名。
注意,在这个白噪声的定义中,我们没有给白噪声的幅值赋予任何的概率分布。如果我们认为白噪音是independent,identically distributed(iid),那么白噪声是一个理想的平稳过程。很多定义默认白噪音是一个平稳过程,我曾经也为定义的问题而困惑。不过后来觉得纠结定义什么的并不重要,从实际角度看,我们最终要处理都要把实际信号当作宽平稳状态过程,即WSS process。有很多定义方面的东西,如果你仔细去思考,你会有很多疑问。很多版本的定义并不能完全把一个东西与另外一个东西区别开来。但死磕这类有工程背景学科的定义会浪费很多时间,相比于严谨科学-数学,我们要从更实际的角度去理解这些定义。
当白噪声通过一个线性系统后,输出便成了有色噪声,即其功率谱不是一个常数,而是随着频率改变发生衰减。对应输出的autocorrelation function也成了一个指数函数,随着 [公式] 的增加而衰减[5,p50]。这再次表明了一个实际线性系统相当于一个low-pass filter。
白噪声本身并没有暗示任何概率分布。现实中噪音的概率分布是不容易得到的。假设一个环境中各个噪音源是独立分布,且来自同一个分布,并且噪音源数量很大,根据中心极限定理(central limit theorem),噪音源的总和也是一个随机变量,并且服从正态分布(Gaussian distribution, or normal distribution)。那么现实中在信号处理的问题中,热噪声(thermal noise, or Johnson–Nyquist noise) 是一种基本的噪音,是由于电子热运动造成的。考虑到电子数量众多,它们共同作用下产生的噪声的概率分布可以认为是Gaussian distribution,而且其功率谱密度不随频率变化而变化,这就是为什么我们可以假设一般噪音是白噪声,并且服从Gaussian distribution的原因之一,这也是处理复杂问题的一种简单有效的方法。如果一个白噪声幅值服从Gaussian distribution,假设其满足各态历经性,那么我们就把它称为高斯白噪声(Gaussian white noise,or additive white Gaussian noise, AWGN)。理想的AWGN是一种平稳的随机噪声(分布不随时间改变),其均值 μ = 0 ,方差为 σ^2 。由于均值为0,我们根据方差的定义:

此时方差就是均方值。由于是各态历经的,我们由均方值 得知,一个均值为0的信号的均方值就是其平均功率,由此推知AWGN的平均功率是无穷大的,即方差无穷大,理想的AWGN根本无法实现(power spectral density仍然是常值,代表的是单位频率上的功率值)。那么为了实现所谓的AWGN,我们必须使其的带宽是有限的,即只有在一段频率上功率谱密度保持常值,这样其自相关函数在 [公式] 处的取值便为有限值,即平均功率为有限值,实际的正态分布方差是有限的:
得知,一个均值为0的信号的均方值就是其平均功率,由此推知AWGN的平均功率是无穷大的,即方差无穷大,理想的AWGN根本无法实现(power spectral density仍然是常值,代表的是单位频率上的功率值)。那么为了实现所谓的AWGN,我们必须使其的带宽是有限的,即只有在一段频率上功率谱密度保持常值,这样其自相关函数在 [公式] 处的取值便为有限值,即平均功率为有限值,实际的正态分布方差是有限的:

根据上式的带限白噪声(bandlimited white noise),我们根据自谱与自相关函数的关系:

(36)在τ = 0时的极限值是一个有限值。根据式(34),我们便知bandlimited gaussian white noise的二阶矩(此处即方差,或者平均功率)是一个有限值,均值为常数0,并且其自相关函数仅与时间τ有关,这符合我们工程中常处理的宽平稳过程,即WSS信号的定义。回过头去看,理想的高斯白噪声由于平均功率无限大,即二阶矩不存在,并不符合WSS的定义。
一个随机过程可以认为有无数个随机变量组成,如果其中任取任意数量的随机变量组成向量,它们的联合概率分布都满足Gaussian distribution,那么这个过程就是高斯过程(Gaussian process)。上面的高斯白噪声,我们假设的是所有噪声源都是独立同分布的(independent and identically distributed),根据中心极限定理,随机变量的和 Wi 最后是呈正态分布的。由于是平稳信号,在每一个时刻 ti , Wi 也服从同一个Gaussian distribution的,我们说高斯白噪声就是一种高斯过程。如同一维正态分布只取决于均值μ和方差 σ^2^,高维正态分布取决于均值向量和协方差矩阵。
参考知识:
如何理解高维正态分布
高斯过程与高斯分布的关系
一阶Markov过程 xt 的下一时刻的概率分布只与上一个时刻的概率分布有关,而与过去的其他时刻的概率分布无关,或者说现在的概率分布和过去所有的概率分布对下一时刻的影响与现在的概率分布对其影响等效。一阶Markov process可以由一阶微分方程,且输入为white noise表示:

如果白噪声是AWGN,那么输出 x(t)为Gauss-Markov Process. 一阶Gauss-Markov process有指数型autocorrelation function ,其中系数β1 的值趋向于0,相当于截断频率越来越低,输出会趋向于随机常数
,其中系数β1 的值趋向于0,相当于截断频率越来越低,输出会趋向于随机常数
线性系统和信号处理理论
我们考虑简单一点的线性时不变系统:

这个系统的全解我们曾经说过,是以下面的式子来计算的:

前面一部分是初值影响的状态量,后一部分是输入引起的状态量。我们之前定义过LTI系统的状态转移矩阵(state transition matrix)为  所以上式也就被重写成了
所以上式也就被重写成了

我们以前也讲过LTI的零状态响应在时域中可以由以下convolution表示:

我们可以定义脉冲响应函数,注意卷积中μ(τ)的积分变量τ是可以和h(t - τ)的t - τ保持卷积值不变的。
现在假设系统的输入是一个random process,统一把输入改为宽平稳(Wide-sense stationary,WSS)随机过程
X(t), ,因为实际中我们多数信号都满足WSS要求。我们已经知道WSS随机过程的均值是常数,自相关函数(autocorrelation function) 只与延时 τ 有关,而与起始时间无关,且二阶矩存在(为有限值)。
两个信号 X(t),Y(t) 被称为jointly WSS, 如果它们都是WSS的,并且互相关函数(cross-correlation function)是时不变的,即只与信号之间的时间间隔有关。
知道了 X(t)的统计特性和功率谱函数,下面来计算X(t)经过系统后的输出 Y(t)的统计特性以及功率谱函数(power spectral density, PSD):
我们考虑LTI系统的输出

输出的期望 E[Y(t)]满足:

注意 h(t) 在频域中就是频率特性或者传递函数H(s) ,利用终值定理可知其稳态时的Gain为 H(0):
输出Y(t)和输入 X(t) 的互相关函数(cross-correlation function) RYX(t,τ):

注:不同定义中关于 RYX 的定义有略微不同,同理也可以定义 RXY ,但本质上我们需要指定一个固定的公式,比如  ,那么
,那么  。这里假设了互相关函数仅与时间间隔有关。上式中使用了
。这里假设了互相关函数仅与时间间隔有关。上式中使用了 的定义。
的定义。
由于X 是WSS过程,我们知道其自相关函数 RXY 只与时间间隔 τ有关(这是个dummy variable,只要当做是一个变量决定了整个函数值就行了)。因此上式也就是:
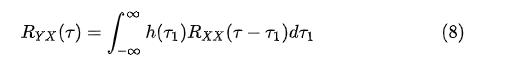
Y(t)的自相关函数(autocorrelation function) 根据定义为

我们发现:

借用(8),我们知道:
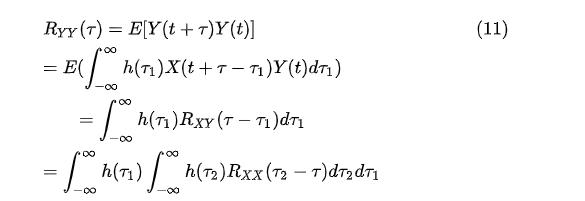 根据维纳-辛钦定理(Wiener–Khinchin theorem), X(t),Y(t) 都是WWS random process,我们把(8)两端进行Fourier transformation,得到 X(t) 与 X(t) 的互功率谱密度函数(cross power spectral density, CPSD) Φ
根据维纳-辛钦定理(Wiener–Khinchin theorem), X(t),Y(t) 都是WWS random process,我们把(8)两端进行Fourier transformation,得到 X(t) 与 X(t) 的互功率谱密度函数(cross power spectral density, CPSD) ΦYX :

根据(11) 我们就得到了Y(t)的自功率谱密度函数(power spectral density)的两种表达式:

注:H(jω)不就是所谓的我们在经典控制理论中的频率特性吗?换言之,也就是传递函数,或者在system identification领域叫frequency response function, FRF。(12)表明,如果我们知道 X(t)的PSD, ΦYX ,以及频率特性或者传递函数 H(jω);H(s) ,那么我们就可以得到CPSD ΦYX。同时这个结论还有一个非常重要的应用,那就是传递函数估计。如果能通过序列估计出CPSD和PSD,我们可以通过:

来估算传递函数,这种FRF的估计方法称为 H1 estimator。有 H1 就有H2,即采用(13)来计算FRF,这两种估计有不同的假设,即前者假设噪音与输入 X(t) 是uncorrelated,后者假设噪音与输出 Y(t) 是uncorrelated。(14)我们放着后面再解释。互谱和自谱的估计,我们在MATLAB中就有cpsd命令帮我们计算,而专门用于传递函数估计的tfestimate函数,也是调用了cpsd,以及采用了上面的公式作为其中一种估计方法。这是一种估计线性系统FRF的非常简单又实用的办法,只需要两个时间序列 Y(t) 和 X(t) 就可以了。详情可以参考
MATLAB documentation - tfestimate
https%3A//web.stanford.edu/class/archive/ee/ee278/ee278.1152/lect08-1.pdf
输出Y(t)的平均功率,满足各态历经假说的前提下,由二阶中心矩给出:

当我们把序列看成是一个n维实数向量 X(t)时,我们有自相关矩阵(auto-correlation matrix)是任意两个时间t1 t2 之间定义的矩阵:

而自协方差矩阵(autocovariance matrix)定义为:
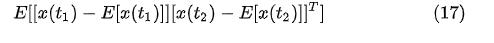
这两者的差别其实就在于autocovariance matrix减掉了X(t) 的期望。如果它的均值为0,即  ,那么自相关矩阵和自协方差矩阵是等价的。至于为什么要写成矩阵的形式,那当然是因为矩阵运算有其独特的优越性。同理我们可以两个随机过程之间的互相关矩阵和协方差矩阵,这个很容易类推就不赘述了。更多阅读见[1,p116-119]。
,那么自相关矩阵和自协方差矩阵是等价的。至于为什么要写成矩阵的形式,那当然是因为矩阵运算有其独特的优越性。同理我们可以两个随机过程之间的互相关矩阵和协方差矩阵,这个很容易类推就不赘述了。更多阅读见[1,p116-119]。
随机线性系统、白化处理
一个连续的线性随机系统(linear stochastic differential equation)一般可以由以下方程表示:

这是一个时变线性系统,所以各矩阵都是时变的。其中 z(t) 是测量输出,与我们以前定义的 y= Cx + Du ,名义上的输出,还不一样(虽然这里还是用C,D矩阵符号了)。在第一行中的 ω(t) 就是一个噪音向量,我们考虑 zero-mean uncorrelated noise process,即均值为0的不自相关的噪音随机过程。显然高斯白噪声(AGWN)是满足条件的。 [公式] 是噪声影响动态的耦合矩阵。而 υ(t) 加入在测量中的测量噪声,我们同样假设是zero-mean uncorreleated的,同样也可以是AGWN。
而实际中我们经常会碰到离散的(discrete)线性随机系统,根据上面的结论,我们可以写出:
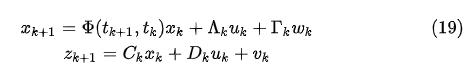
其中  为transition matrix,
为transition matrix, ,
,
 .
.
为什么我们在模型中总假设噪音都是Gussian white noise呢?实际中的噪声常常都是有色噪声,即power spectral density并不总是为常数的随机噪声。上一篇中我提到了,当白噪声通过一个线性系统时,其输出是有色噪声。因此,已知有色噪声的PSD或者autocorrelation function,假定它是高斯白噪声通过某个线性系统后产生的输出,是否可以反向推出这个线性系统的模型呢?答案是肯定的。通过一个特定的线性系统,称之为"shaping filter"[1,p131],使得白噪声变成了需要的有色噪声,我们就可以把这部分动态的模型包含到原有系统的建模中。这使得我们可以把原来系统动态中的有色噪声,替换成白噪声和shaping filter的模型。
我们举一个时域连续系统的例子来说明。
当高斯白噪声通过一个一阶稳定线性系统时,其输出为一个自相关函数为指数函数的有色噪声。现在我们假设有色噪声的autocorrelation为:

其对应的PSD,满足宽平稳过程WSS的条件下,就是它的Fourier Transformation:

我们把这个有色噪声当做 Y(t) ,把高斯白噪声当做 X(t) ,服从标准正态分布,即方差  为1,均值
为1,均值  为0。那么 X(t) 的自功率谱密度函数
为0。那么 X(t) 的自功率谱密度函数  ,其自相关函数为
,其自相关函数为  。根据公式(11):
。根据公式(11):
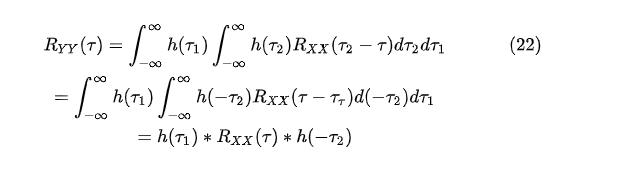
其中 [公式] 代表了convolution运算。这个结论正是公式(14)的来源。我们把(22)两端进行Fourier Transform,得到了线性系统输出的自谱和输入的自谱关系:

那么现在代入  ,我们得到了:
,我们得到了:

取稳定的频率特性,便有了这个我们需要的shaping filter,即一个想象中假定存在的系统:

这就是把标准正态分布的高斯白噪声转化为autocorrelation为(20),或者自谱为(21)的特定filter,我们可以把它写成时域微分方程:
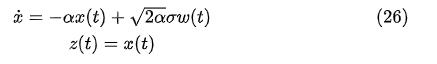
我们说shaping filter (26)的输出 z(t) 正是有色噪声 Y(t) ,而输入则是高斯白噪声 ω(t) 。注意这里我们替换了符号,采用了熟悉的x 作为状态, ω(t) 作为噪声。有了(26)之后,我们便可以对有色噪声进行替换,比如状态空间方程:

其中 ωy(t)是有色噪声,其autocorrelation满足(20)。那么我们 incorporate (26) into (27),得到:

把(27)重新写成成新的状态空间表达式就不是什么难事了,所谓的augmented state space。我们这种将有色噪声输入转化为等效白噪声输入的过程也称之为白化处理。离散系统的做法并不一样,可以参考[1,p129, Example 4.4],不过背后的想法是一样的。
Classic estimation theory 经典估计理论
估计是用过去到现在的数据来计算现在的某个量的大小。估计理论主要还是属于概率与统计学领域。我们知道统计学有两大学派:频率学派(frequentist statistics)和贝叶斯学派(bayesian statistics)。估计理论也可以根据这两个学派不同的观点分为经典估计理论和贝叶斯估计理论。 经典的估计理论我们在以前上统计学课程的时候应该已经接触过了,主要在参数估计那一块,包括点估计和区间估计两大类,其中有比如最大似然估计算法,一致最小方差无偏估计等。我们抽里面的重点进行回顾和讲解,目的是为了和后面的贝叶斯估计有一个对比。Kalman filter的推导用到的估计知识,主要是后者。对比两种估计理论的不同点,有利于加深记忆。统计推断(statistical inference)的任务是要通过研究样本数据来分析总体的特征。总体是由分布描述的,现实中很多时候容易知道分布的类型,但却不知道其参数。那么如何从样本数据中得到分布的参数是关键问题,即参数估计(parameter estiamtion)。值得注意的,参数估计和状态估计问题还不能完全等同起来,这点随着知识不断扩展慢慢体会。
Unbiasedness and consistency 无偏性与相合性
我们下面都以 θ 来作为未知参数。频率学派认为,未知参数 θ 的真值是一个确定的值(deterministic)。根据总体中的抽样样本 x1,x2,...xn ,构造一个统计量(statistic):

称之为 θ 的估计量(estimator),或叫 θ 的点估计(point estimator),简称估计——点估计的名字是因为最后估计量的取值是一个数,与区间估计相对。统计量  是一个样本的函数(统计量的定义),也是一个随机变量(因样本具有随机性)。
是一个样本的函数(统计量的定义),也是一个随机变量(因样本具有随机性)。
注:统计量  本身是一个函数,但很多地方符号本身也表示了其取值,类似于 y = y(x)这么个意思。注意英语中的用词,estimator表示的是估计量,即统计量,其为样本的函数。estimate是estimator在某个样本处的取值,是根据取得的样本给出的估计值。
本身是一个函数,但很多地方符号本身也表示了其取值,类似于 y = y(x)这么个意思。注意英语中的用词,estimator表示的是估计量,即统计量,其为样本的函数。estimate是estimator在某个样本处的取值,是根据取得的样本给出的估计值。
θ 的估计可以构造无数种,估计之间孰优孰劣,需要一些标准来评判。我们说一个估计是unbiased(无偏的),是指这个估计的期望值与对所有可能的被估计量 θ 的真实值一样:

Θ是 θ可能的取值空间,称参数空间。无偏性(unbiasedness)告诉了我们这个估计  是在真值 θ 周围波动的,但如果我们求平均(期望)之后,最后等于真值。除非是
是在真值 θ 周围波动的,但如果我们求平均(期望)之后,最后等于真值。除非是  的线性函数,一般
的线性函数,一般  的函数
的函数  是不会继承其无偏性的,比如修正样本方差 s^2^ 是无偏的,但是开平方根的s 却是有偏的(biased)。 在其他评判标准满足时,存在无偏估计时,应当尽量使用无偏估计,这意味着估计从原理上就不存在偏差。有些估计,如样本方差
是不会继承其无偏性的,比如修正样本方差 s^2^ 是无偏的,但是开平方根的s 却是有偏的(biased)。 在其他评判标准满足时,存在无偏估计时,应当尽量使用无偏估计,这意味着估计从原理上就不存在偏差。有些估计,如样本方差  本身是有偏的,但随着样本数增加,它可以满足渐进无偏性(asymptotic unbiasedness),在大样本时是可以近似认为无偏的。一个拥有较大bias的估计认为是有缺陷的,一般是不会采用的。不是所有参数都存在无偏估计,若 θ 存在unbiased estimator,则称其是可估的(estimable)
本身是有偏的,但随着样本数增加,它可以满足渐进无偏性(asymptotic unbiasedness),在大样本时是可以近似认为无偏的。一个拥有较大bias的估计认为是有缺陷的,一般是不会采用的。不是所有参数都存在无偏估计,若 θ 存在unbiased estimator,则称其是可估的(estimable)
随着样本量 n 的增加,我们希望估计量不断逼近参数真值,这种性质称为consistency(相合性)。把 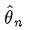 看成是随着n变化形成的随机变量序列,则
看成是随着n变化形成的随机变量序列,则 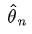 依概率收敛到 θ 。判断相合性一个常用的充分条件是:若
依概率收敛到 θ 。判断相合性一个常用的充分条件是:若  则
则 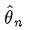 是consistent estimator. 相合性是统计量的一种大样本性质。无偏和相合是两个不同的概念。相合性被认为是很基本的要求,如果某些场合只存在有偏估计,那么至少也要采用一个相合的估计。
是consistent estimator. 相合性是统计量的一种大样本性质。无偏和相合是两个不同的概念。相合性被认为是很基本的要求,如果某些场合只存在有偏估计,那么至少也要采用一个相合的估计。
method of moments 矩法
常用和常见的一种估计方法是矩法(method of moments),其思想使用样本矩(sample moment)去替换总体矩(population moment),然后通过样本矩反推总体分布的参数值。其背后的思想基于格里汶科定理——经验分布函数随着样本增加接近总体分布。根据这个方法,即便有些时候分布形式是未知的,我们依旧可以估计一些参数:比如用样本均值  和样本方差
和样本方差 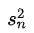 估计总体均值 μ (一阶原点矩 E(x) )与总体方差σ^2^ (二阶中心矩 E(E - E(X))^2^) 。在分布和概率函数形式已知时,我们可以写出该随机变量 x 的 k 阶矩表达式(以原点矩为例):
估计总体均值 μ (一阶原点矩 E(x) )与总体方差σ^2^ (二阶中心矩 E(E - E(X))^2^) 。在分布和概率函数形式已知时,我们可以写出该随机变量 x 的 k 阶矩表达式(以原点矩为例):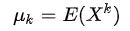 ,它们应当是概率函数中未知参数
,它们应当是概率函数中未知参数 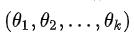 的函数。用样本原点矩
的函数。用样本原点矩  代替 μ
代替 μk 就可以列出 k 个方程来求解 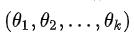 。此法简单实用,不过不一定得到无偏估计量,但一般满足相合性。
。此法简单实用,不过不一定得到无偏估计量,但一般满足相合性。
Maximum Likelihood Estimation(MLE) 最大似然估计
MLE(最大似然估计,或极大似然估计)是非常传统的频率学派估计方法,当然学过了Bayesian estimation之后,我们又把它当作了一种maximum a posteriori (MAP) estimation的一种特例。MLE背后的思想非常简单易懂的:认为已经发生的事情是最有可能发生的。
相信各位已经看厌了投硬币的例子,那我编个让各位感同身受的例子:你通常喜欢在打游戏时反锁家门。上个月由于天天把家门反锁打游戏,被你爸发现骂的狗血淋头。这个月开始你洗心革面,决定不打游戏了,天天在家里看知乎学习。结果今天不小心你又把家里门给反锁了,傍晚爸爸回家看到了门被反锁,问他是相信你当天在打游戏还是没打游戏?
基于复数的概念的正交信号,以及与正交信号相关的许多如j-operator(算符、算子)、complex(复数的)、imaginary(虚部的)、real(实部的),以及orthogonal(正交的)等专业术语,可能会比其他的课程习题更能令数字信号处理专业的初学者们感到头疼。
如果你有点不确定复数和j=sqrt(-1)(-1开平方根)算子的实际物理意义,没关系,请你不要感到悲伤。因为,甚至是世界最伟大的数学家之一的Karl Gauss(高斯),也曾把j-operator叫做“影子中的影子”。今天在这篇文章当中,我们会剖析这个“影子中的影子”,那样,你就再不用打“正交信号心理热线”求助了。
正交信号处理被广泛用于科学和工程领域,并且用于描述现代数字通信系统中的处理方法和实现。在本文的指导教程中,我们会回顾复数的基础知识,并且理解复数是怎样用于表示正交信号的。接下来,我们会复习正交信号代数符号中负频率的概念,并且,学习使用正交处理的专业术语。另外,我们将用三维的时-频图来解释正交信号的一些实际物理意义。这本文指导教程的最后,简要介绍了怎样通过正交采样的手段生成正交信号。
正交信号,也被叫做复信号,在很多数字信号处理应用中被使用,例如:
- 数字通信系统
- 雷达系统(重点)
- 无线线电测向系统中的到达时间差处理
- 相参脉冲测量系统
- 天线波束形成应用
- 单边带调制器
- 其他
上述这些应用都属于正交处理的一般范畴,并且通过实现正弦信号相位的相参测量来提供额外的处理能力。一个正弦信号是一个二维的信号,这个二维信号在某时刻的瞬时值可以用一个有两个部分组成的复数来表示,这两个部分即我们所说的实部和虚部。
注:real和imaginary 两词很传统,在日常中的意思使它们在这里的使用显得有点不太合适。因此,通信工程师们会使用同相相位和正交相位两个术语,后边更多的使用这两个术语的地方。下面让我们一起来回顾这些复数的数学表示。
复数的发展
和表示为了建立复数的概念,这里定义一个我们在日常生活中使用的实数数字,如一个电压、一个华氏温度,或是你支票账户的结余。这些一维的数字既可以是正的,也可以是负的,见图1(a)。在图中我们展示了一个一维的数轴,并一个实数可以用数轴上的一点来表示。通常,我们把这个坐标轴叫做实轴。
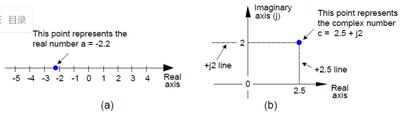
在图1(b)中,复数C也被表示为一个点。但是,复数C并不止坐落在一条一维线上,而是位于一个二维平面中的任何地方。这个平面被叫做复数平面(简称复平面或复数域,一些数学家喜欢把它叫做阿尔干图),复平面给我们提供了一种表示既有实部又有虚部的复数的方法。
例如,在图1(b)中,复数C=2.5+j2 是一个位于复数平面中的既不在实轴也不在虚轴上的点。我们通过沿着实轴走+2.5个单位,再沿虚轴向上走+2个单位来定位点C。你可以把实轴和虚轴看作是地图上的东西方向和南北方向。
下面我们将用一个几何学的观点来帮助我们理解一些复数的计算。如下图2所示,我们用直角三角形的三角原理来说明几种不同的表示复数C的方法。

在一些文献资料中,复数C被许多的不同方式来表示,例如:

表中公式(3)和(4)表明复数C也可以被认为是复平面上一个相量的末端,幅度为M,方向为Φ度(相对于正实轴),如图2所示。记住,C是个复数,而变量a,b,M和Φ都是实数。
C的幅度,有时被称做C的模,即:

相位角Φ,或者幅角,是虚部实部比的反正切值,表示为:
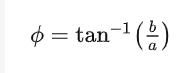
如果我们令公式(3)等于公式(2)
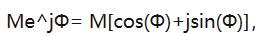
得到欧拉恒等式之一,我们致敬欧拉并以他的名字命名公式,如下:

疑心的读者应该正在质问:“为什么采用那个用自然对数的底e的奇怪表达式来描述一个复数是有效的,这十分令人难以想象?”
我们可以像世界最伟大的无穷级数数学家欧拉那样证明公式(7),通过给图3的顶上那行里的e^z的级数展开表述中的z代入jΦ,这个代入展示在第二行。接下来,我们求j的高次值得到图中第三行的级数。你们中那些像欧拉那样高的数学技巧(或者那些查过一些数学参考书)的人会在第三行里认出那些交替的项就是cosine和sine函数的级数展开表达式。

图3证明了公式(7)和我们用公式(3)极坐标形式(Me^jΦ)对复数的表述。图3的第一行中,如果你用-jΦ来替换z,最终你会得到一个稍有不同的,并且很有用的欧拉公式形式:

上面公式的极坐标形式对我们有好处是因为:
- 它简化了数学的推导和分析把三角法的公式转换成简单的指数的代数,并且复数的数学运算得以遵照与实数同样的规则。
- 它让信号的相加只是复数的相加(矢量相加)
- 它是最简洁的表达方式
- 它表明了数字通信系统是如何实现的,并且在文献中进行了描述
我们将用带极坐标变量的公式来理解正交信号是为什么要在数字通信应用中被使用,并且是如何使用的。
但首先,让我们深吸一口气,因为现在进入了j算子的模糊区域。之前,你已经看到了j=sqrt(-1)的定义,通俗地讲,我们说j是代表一个乘以自己等于-1的数,这个定义会给初学者造成困惑,因为我们都知道任何数的平方总是到一个正数。
遗憾的是,数字信号处理课本经常定义j,然后,学生们带着看似合理的轻率,并迅速的熟悉了与j算子用于分析正弦信号的各种方法。
但是读者们很快忘了那个问题:j=sqrt(-1)到底意味着什么?其实,sqrt(-1)曾经在数学领域出现过一段时间,但那个时候并没有被大家认真对待。
直到16世纪的时候,它不得不被用于解决三次方程(cubic equation),数学家们才开始并有些不情愿地接受sqrt(-1)的抽象概念,但并不没有将其形象化,因为它的数学特性与一般实数的计算是一致的。
后来,数学家欧拉把复数和真实的正弦及余弦联系起来,然后高斯巧妙地引入了复数平面,最终在18世纪,使sqrt(-1)的概念有了合法的地位。
超越了实数领域的欧拉,证明了了复数和我们熟知的正弦和余弦实三角函数有着极为巧合的关系,如同爱因斯坦提出的质和量的等价关系一样。
不过,欧拉虽然证明了实正余弦函数与复数的等价,但人们对于
这个等价关系的理解如同现代的物理学家们不知道什么是电子,但能理解它的特性一样。
(这句话非常有哲理,体现了目前我们人类对于物质认识的程度仅限于只知道现象,而并不知道其本质!)因为我们人类对某些物理现象还没有一个合理的解释,因此我们不用担心j是什么,而只需要理解它们的作用就够了。
对于我们来说,j算子表示把一个复数逆时针旋转90度。让我们来看为什么这样。如图4所示,通过测试j=sqrt(-1)算子的数学特性,我们将习惯用复数的复平面表示。

如图4所示,j乘以任何一个实轴上的数会得到一个位于虚轴上的虚的产物。图4中的例子中,+8被用位于正实轴上的一个点表示,+8乘以j得到一个虚数,+j8,与+8相比,在复平面中的位置被逆时针旋转了90度,位于正虚轴。
类似的,因为j^2=-1,+j8乘以j将引起另一个90度旋转,得到了位于负实轴上的-8。-8乘以j引起进一步的90度旋转得到位于负虚轴上的-j8。
不论何时一个用点表示的任意数字乘以j,结果都是90度的逆时针旋转。(相反的,乘以-j,就引起复平面上的90度顺时针旋转。)如果我们令公式7中的Φ=π/2,我们得到:
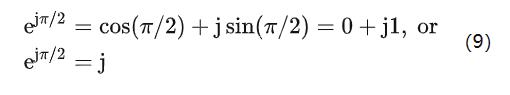
不过,这里有一点要记住,在复平面上的一个用点表示的复数,乘以j或者e^(jπ/2)会引起逆时针90度旋转而得到一个新的复数。
别忘了这个,因为它会在你开始阅读正交处理系统文献的时候有用。让我们暂停一会儿,来歇一口气,缓缓脑子,消化一下之前的内容。如果虚数和复平面的概念看起来有点难以理解,别担心,任何人刚开始都是这个样子。你越多用它们,你会越习惯它们。
记住,j算子是曾使欧洲的重量级数学家们迷惑了数百年的东西,必须承认,刚开始的时候,不仅是复数的数学有点奇怪,其专业术语也十分古怪。
用复相量表示实信号
现在,我们把注意力放在是时间函数的复数上。
假设一个信号,它的幅度是1,而且它的相位角随时间增大。这个复数就是图5(a)上的那个点e^(j2πf0t),这里,2πf0是以弧度/秒为单位的频率w,并且它与以赫兹(即周/秒)为单位的频率f0是相同的。
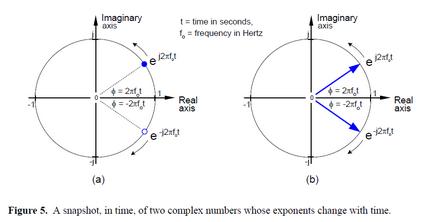
随着时间t增大,这个复数的相位角也会增大,并且绕复平面的原点按逆时针方向做圆周运动。
图5(a)上,该复数用蓝色实心点表示,在某一任意瞬时时刻静止。如果f0=2Hz,那么,那个蓝色实心点会按照每秒两圈的频率绕圈。
我们也可以考虑一下另一个复数e-j2πf0t (蓝色虚心点表示),它将随时间的增长,顺时针绕圈。现在,让我们把e^(j2πf0t)和e^(-j2πf0t)两个复数表达式称作正交信号。它们各自都拥有实部和虚部,并且都是时间的函数。
在文献中,这两个表达式经常被称作复指数(complex exponentials)。我们也可以把这两个正交信号,e^(j2πf0t)和e^(-j2πf0t),当作是图5(b)中两个按相反方向旋转的矢量的末端。目前,我们将继续使用这个相量表示,因为它可以在复平面的背景中描述实正弦信号。为了确保我们能够理解这些相量的作用,图6(a)显示了相量e^(j2πf0t)随时间变化的三维轨迹。我们加入了时间轴来显示该相量的螺旋形轨迹。
图6(b)显示了仅有相量e^(j2πf0t)的末梢的连续形式。
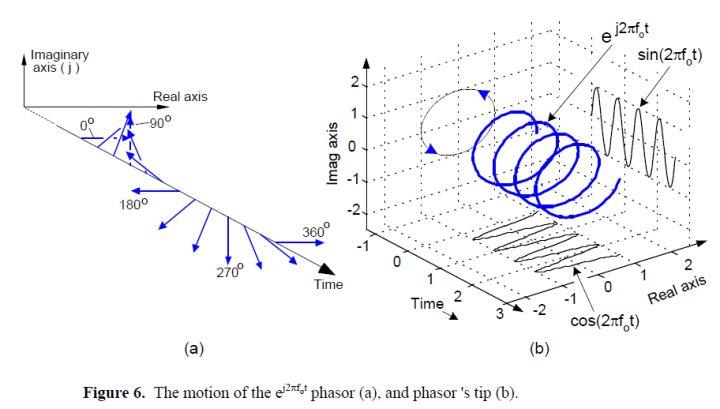
复数e^(j2πf0t),可以叫做相量的末端,以时间轴为中心,沿着螺旋形轨迹向由里及外延伸。 图6(b)中,e^(j2πf0t)的实部和虚部就是正弦和余弦投影。 (重点内容!读者要记住!)回到图5(b)中,问你自己:这两个沿反方向旋转的相量的矢量和是什么?考虑一会儿…,对了,相量的实部会总是同向相加,而虚部总是会抵消。
这就意味着相量e^(j2πf0t)和e^(-j2πf0t)相加总是会得到一个实数,现代数字通信系统的实现就是基于这一特性
(重点内容!读者要记住!)为了强调这两个复正弦曲线的实数和的重要性,我们再画另一幅图,如图7中所示的三维波形,它由e^(j2πf0t)和e^(-j2πf0t)这两个以时间轴为中心沿相反方向旋转伸展的半幅度复相量相加得到。
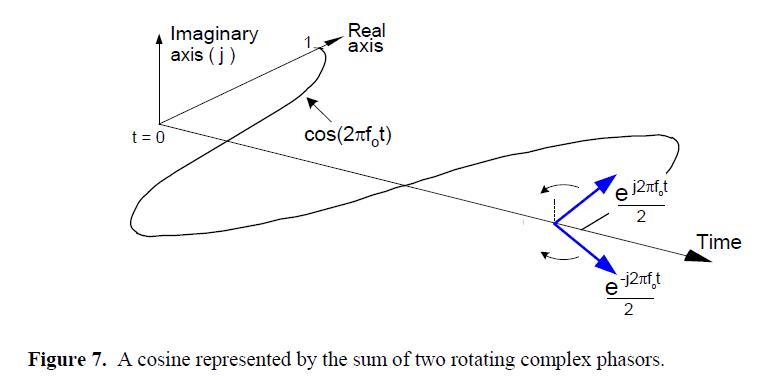
思考下这些相量,现在很明确,为什么余弦曲线可以等价于两个复指数的和,是怎么得到的。

公式(10),一个著名的重要表达式,也被叫做欧拉等式之一。我们可以通过对公式(7)和(8)求解jsin(Φ)来得到这个等式,使这两个表达式相等,从最终等式中求出cos(Φ)。类似的,我们可以把同样的代数练习做完并且得到,一个实正弦波形也是两个复指数的和,如下:

仔细看公式(10)和(11),它们是余弦波形和正弦波形的标准表达式,使用复数形式表示,在正交通信系统的文献中很常见。为了避免读者的思维像那些复相量一样旋转,请明确,公式(5)到(7)的目的只是用以证明公式(10)和(11)中得到的余弦和正弦波形的复数表达式。这两个公式,连同公式(7)和(8),是正交信号处理的罗塞达石(Rosetta Stone,是解释古埃及象形文字的可靠线索)。

我们现在可以轻松地在真实正弦曲线和复指数之间来回转换。同样,我们正在学习如何通过同轴电缆传输真实信号或将其数字化并存储在计算机的内存中,可以用复数符号来表示。是的,复数的组成部分都是实数,但我们将这些部分以特殊的方式处理,即我们正在正交地处理它们。
频域的正交信号表示
关于正交信号的时域特性,现在我们已经知道得足够多了,那么我们准备好了去接受它们的频域描述。
因为我们将阐明其频域的全部三维特性,正交信号的任何一个相位关系都不会被隐藏,所以这部分的文章会很容易理解,图8告诉了我们频域中复指数的表达规则。

我们将把一个复指数表示成一个由幂指数上的频率f确定的窄带脉冲。另外,我们将沿实轴和虚轴说明这些复指数之间的相位关系。为了阐述这些相位关系,一个复频率域(复频域)表示是必须的,如图9所示。
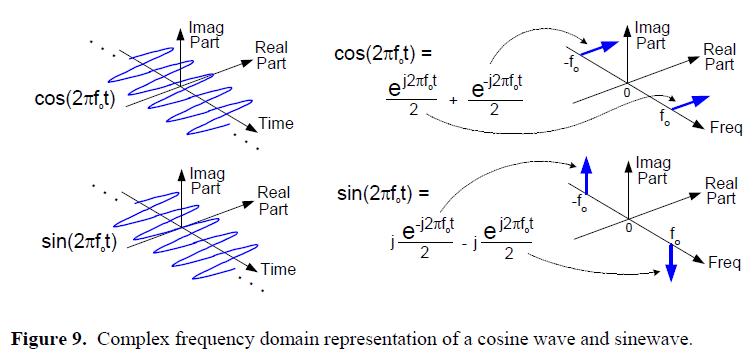
在图9的右边,可以看到实余弦波形和正弦波形是如何在复频率域表示中被描述的。那些粗箭头不是旋转着的相量,而是表示复指数e^(j2πf0t)的单根谱线在频域的脉冲信号。谱脉冲的方向指向仅指示频谱组成的相对相位,这些谱脉冲的幅度是1/2。
为什么我们会跟这个三维坐标的频域表示纠缠这么久?
因为这是我们将用以理解数字(及一些模拟)通信系统中正交信号的生成(调制)和检测(解调)的工具,这也是本文的目标中的两个。在我们考虑这些处理之前,让我们用个小例子来证明这个频域表达。
如图10,是个说明我们如何使用复频率域的简单例子。这里我们从一个正弦波开始,将j算子代入,然后把结果与同频的实余弦波形相加。最终,在公式(7)中的欧拉等式被图形化阐释,得到复指数e^(j2πf0t)。
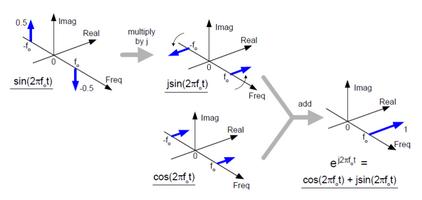
在频率轴上,负频率的概念在这儿被看做位于频率轴-2πf0弧度/秒处的谱脉冲。这幅图说明了重要的结论:当我们使用复数概念,像e^(j2πf0t)和e^(-j2πf0t)这样的复指数是实正弦曲线sin(2πft)和cos(2πft)的基本构成部分,这是因为sin(2πft)和cos(2πft)都由e^(j2πf0t)和e^(-j2πf0t)作为部分构成。
如果你对正弦波sin(2πf0t)、余弦波cos(2πf0t)或者e^(j2πf0t)的复正弦波形的离散时域采样值进行离散傅里叶变换(DFT),并且把复数结果作图,你就能得到图10中的窄带脉冲。
频域带通正交信号
按照惯例,在正交处理中,频谱的实部被叫做同相分量,虚部被叫做正交分量。图11(a),(b),(c)中的信号的复数谱是实数的,且在时域中,它们能够被表示为有非零实部和零值虚部的数。在时域,信号是实数的,我们并不一定要使用复数形式去表示它们。
实数的信号总是有正的和负的频谱分量,任何一个实数的信号,其同相频谱的正和负的频率分量总是以零频点为中心对称,即同相分量的正和负的频率分量互为镜像。
反过来说,正交分量频谱的正的和负的频率部分总是相反。这意味着任何正交正频率分量的相位角与对应的正交负频率分量是相反的,如图11(a)中的细实线箭头所示。当频谱被用复数形式表示时,这种成对的对称是实数信号不变的特性。

让我们再次提醒自己,图11(a)和(b)中的那些粗箭头不是旋转着的相量,而是表示复指数e^(j2πf0t)的单根谱线的频域脉冲符号,谱脉冲的方向指向仅指示频谱分量的相对相位。
在我们继续之前,这儿有个重要准则必须要记住。如图12(a)和(b)所示,一个时域信号乘以复指数e^(j2πf0t),该信号的频谱将被向上搬移f0Hz,这个过程我们叫做正交混频(quadrature mixing)(也叫做复调制complex mixing)。同样,一个时域信号乘以e^(-j2πf0t),将把信号频谱向下搬移f0Hz。
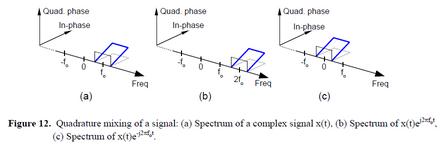
下面是一个正交采样的例子,我们可以通过探索正交采样的处理来使用我们之前学习到的关于正交信号的所有知识。
正交采样是一个数字化一个连续(模拟)带通信号并且将其频谱搬移至0Hz(零中频)的过程。让我们通过设计一个以fcHz的载波频率为中心,带宽为B的连续带通信号,来看这个过程是如何工作的。
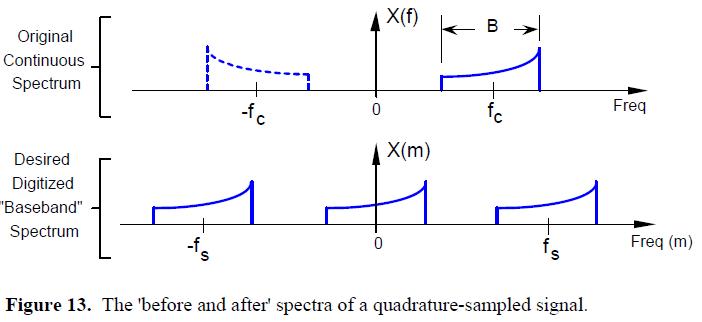
在正交采样中,我们的目标是得到该模拟带通信号的数字量化值,并且这个数字化信号的离散频谱以0Hz为中心,而非fcHz。那么,我们通过将这个时域信号乘以e^(-j2πfct)来实现复数的向下转换。
频率fs是数字转换器(ADC)的采样速率,单位为samples/second。在图13的最下行中的重复的频谱只是来提醒我们当A/D转换发生时的效果,即在时域采样等同于在频域进行以w_s为周期的延拓。图14顶部的结构图,就是称作I/Q解调(有通信理论经验的人称为“Weaver demodulation)的正交采样的框图。
安装的相位相差90度的两个正弦波振荡器通常被称作正交振荡器。
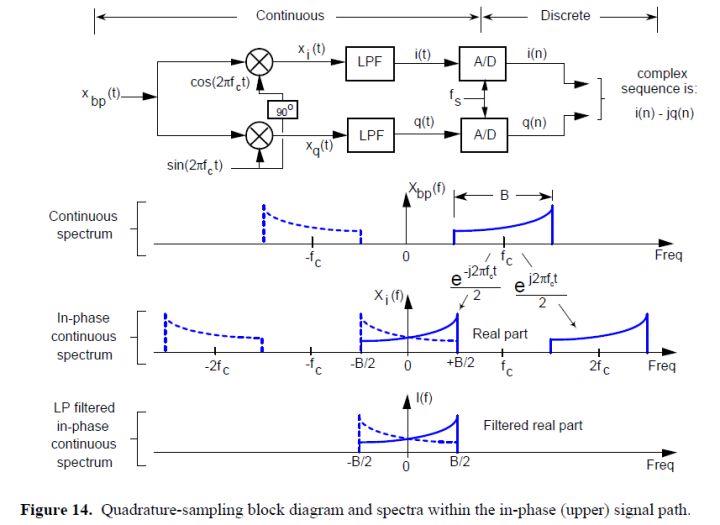
复杂的图14中的e^(j2πf0t)和e^(-j2πf0t)提醒我们,包括一个实数余弦的组成的复指数,复制了Xbp(f)频谱的每个部分来产生Xi(f)。上面这幅图说明了我们如何得到我们所需的复正交信号的滤波后的连续同相部分。
本质上,Xi(f)和I(f)频谱都被当做实数处理。(噪声电平会叠加)同样的,图15告诉我们如何通过将Xbp(t)和sin(2πfct)来得到复正交信号滤波后的连续正交相位部分。
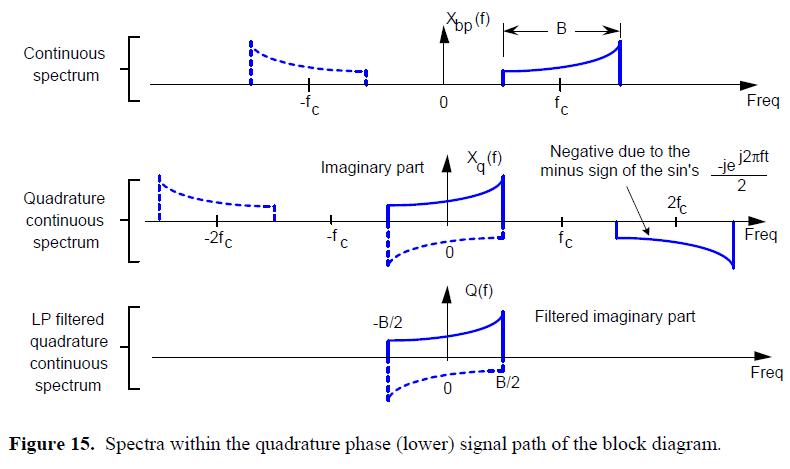
这里我们继续:I(f)-jQ(f)就是我们原先的带通信号Xbp(t)的复制品的频谱,图16说明了两个频谱的相加。
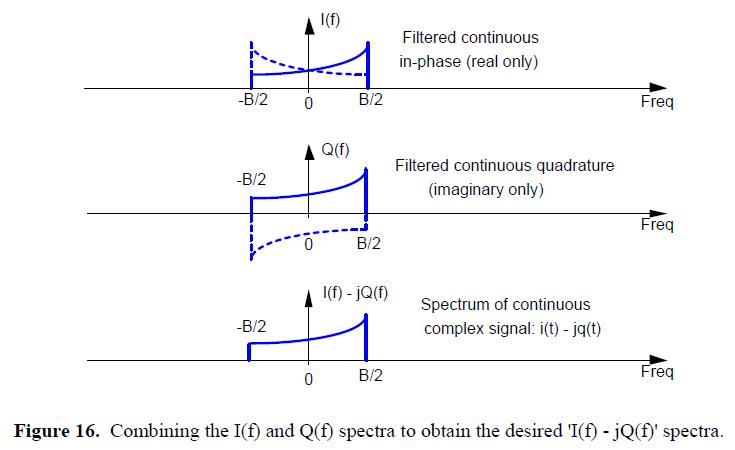
这个典型的正交采样的描述看起来令人迷惑不解,直到你用一个三维的观点看待这个情况,如图17所示。其中,-j算子将仅虚部的Q(f)旋转了-90度,使其变成仅实数的。然后,I(f)和-jQ(f)相加。

图18底部的复数频谱就是我们需要的:中心频率为0Hz的复数带通信号的数字化形式。(相参噪声电平不会增加)

正交采样方式的一些优点: - 每个A/D转换器的工作采样率是标准实信号采样速率的一半。 - 硬件工作在较低的时钟速率下可以节省能源。 - 对于指定的采样率,我们能捕捉更大带宽的模拟信号。 - 得益于更宽的频率范围覆盖,正交序列可以使FFT处理更加有效。 - 由于正交序列通过两个通道被有效的过采样了,这使信号的平方运算在不需要upsampling(上采样)的情况下成为可能。 - 确定信号的相位便于相参处理,并且正交采样也让解调过程中信号的瞬时幅度和相位测量变得简单。
回到框图,别忘了正交信号的一个重要特性。我们能够将模拟正交信号进行远距离传输。我们使用两根分别传输实数i(t)和q(t)的同轴电缆来实现这个。(为了实现离散时域正交序列的传输,我们需要两根多导体带状电缆(multi-conductor ribbon cables),见图19。
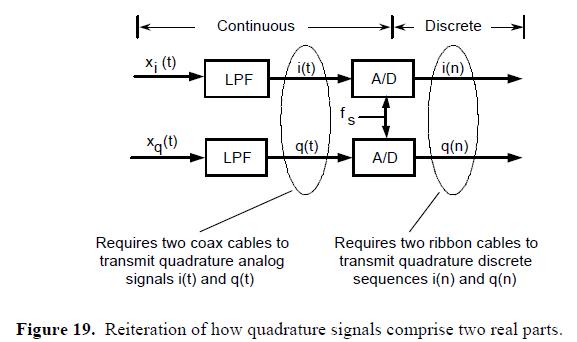
接下来我们链接同轴电缆,将电缆链接到发电机的输出连接器并运行这两条电缆,为余弦信号标记i(t),正弦信号标记q(t),沿着大厅到达目的地。
现在,进行两个问题测试试验。在另一个实验室,我们会在屏幕上看到示波器显示什么,如果连续信号i(t)和q(t)链接到水平和垂直输入通道。(记住,设置示波器水平扫描控制到“外部”位置)。
两个问题测试: 这个测验很简单,只有两个问题,是由学校心理学家杰克·菲南做的。不同的反应组合构成了不同的结果。该理论的基本原理是,玩家不需要通过许多问题来发现自己是哪所学院,而是通过两个问题来揭示自己的道德。所以根据你选择的答案组合,为你选择一所学院。

接下来,如果电缆贴错标签并且两个信号被无意交换了又怎么样呢? 第一个问题的答案是:我们会看到一个亮点逆时针旋转,示波器显示屏幕上的圆,如果交换电缆,则会看到另一个圆圈,但这次是顺时针旋转。
如果我们设置好信号发生器的频率为1Hz,这将是一个简洁的演示(读者可自行实验)。这个示波器实验帮我们回答了一个更重要的问题:当我们使用正交信号,j算子是如何在硬件中实现的?答案是:j算子是通过我们如何处理这两个信号之间的相对关系来实现的,我们必须让他们的同相i(t)信号代表一个东西方的值,并且正交相位q(t)信号表示正交南北方的值。因此,在我们的演示实验示波器中,j算子仅通过链接方式来实现,同相i(t)信号控制水平偏转,正交q(t)信号控制垂直偏转,结果是一个由示波器显示屏上圆点恶瞬时值表示的二维正交信号。
为了充分理解我们这里的讨论的实际意义,让我们记住,一个连续的正交信号Xc(t)=i(t)+jq(t)不仅仅是个数学抽象。
我们可以在我们的实验室里生成Xc(t)并把它传到走廊头上的实验室。走廊那头的实验室接收信号的人说,离散序列i(n)和q(n)可以通过加或减jq(n)来控制最终复数频谱的方向,见图21.
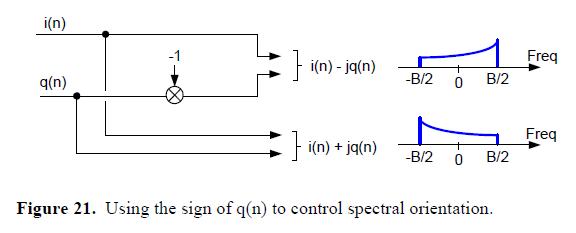
图21的上部的路径等同于把原始的Xbp(t)乘以e^(-j2πf0t),而底部的路径等同于将Xbp(t)乘以e^(j2πf0t)。
因此,使图14顶部的正交振荡器的正交分量变负,-sin(2πfct),合成的复数频谱会像图21中所示的那样以0Hz为中心产生翻转。当我们在考虑翻转着的复数频谱的时候,让我们提醒自己,有两个简单方法来使x(n)=i(n)+jq(n)的序列的频谱幅度产生翻转,如图21所示。第一种方法是,我们可以通过使用共轭来得到频谱幅度翻转的序列X’((n)=i(n)-jq(n)。第二个方法就是交换X(n)序列的子列i(n)和q(n)的采样值来生成一个新的序列y(n)=q(n)+ji(n),这个新序列的频谱幅度与X(n)的频谱幅度是相反的。
(注意,当X(n)和y(n)的频谱幅度相等时,它们的频谱相位不相等。)
希尔伯特变换的物理意义十分简单:把信号的所有频率分量的相位推迟90度。
也就是说,如果原信号可以表示成

则经过希尔伯特变换后的信号为
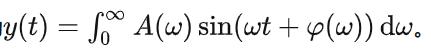
这一点通过希尔伯特变换的频域形式很容易看出来:
希尔伯特变换的物理意义十分简单:把信号的所有频率分量的相位推迟90度。
也就是说,如果原信号可以表示成

则经过希尔伯特变换后的信号为
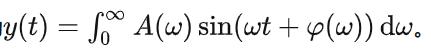
这一点通过希尔伯特变换的频域形式很容易看出来:
这一点通过希尔伯特变换的频域形式很容易看出来:

把相位推迟90度有什么用?
答案是:希尔伯特变换可以用来做解调器,调幅、调频都能解。
如图,蓝色x(t)是一个调制信号
,其幅度、频率都经过了调制。

绿色y(t)是蓝色信号的希尔伯特变换
。由于调制波的幅度和瞬时频率变化都很慢(与载波频率相比),其频率成分比较单一(都集中在载波频率附近),所以希尔伯特变换的效果——相位推迟90度——是很明显的。

现在构造信号 ,我们想办法把这个信号在三维空间中画出来。
,我们想办法把这个信号在三维空间中画出来。
下面这张图中有三个轴:时间轴、实轴、虚轴。时间轴和实轴构成的平面上画出了x(t)(蓝色),时间轴和虚轴构成的平面上画出了iy(t)(绿色)
三维空间中画出了z(t)(红色)。可以看出,z(t)的样子就像一根粗细、疏密都在变化的弹簧。

在任意一个时刻,我们都可以读出z(t)的瞬时幅度和瞬时相位:
瞬时幅度为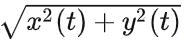 ,瞬时相位的正切值为
,瞬时相位的正切值为

而瞬时相位对时间的导数就是瞬时频率。
这样,我们就利用希尔伯特变换从一个幅度、频率均被调制的调制波中把幅度、频率都解调了出来。
当然,实际的解调器中并不是这么做的,一个重要的原因就是希尔伯特变换不是因果的,不能实时解调。
卡尔曼滤波做的事就是:举个例子,已知上个时刻飞机的位置,知道现在这个时刻收到的雷达测量的飞机的位置。用前面两个数据来估计此时飞机的位置。精简的说就是知道上个时刻状态,又知道测量数据,融合这两个数据来求当前状态。
你一定会问现在知道当前时刻的测量数据那么我认为当前状态就是测量数据不就好了么?换句话说:“你一定会觉得雷达测量到的飞机位置不就是当前飞机的位置嘛?为何要用卡尔曼滤波来估计飞机当前的位置?”。
答:现在这个时刻收到的雷达信号测量的飞机的位置还真不一定是飞机当前的真实位置。首先雷达信号测量有误差。其次你想想我现在收到雷达信号,那是之前发射过去然后返回的信号。这个过程是不是要时间?这段时间飞机说不定以超2倍音速飞行,说不定直接坠机,这些都有可能。也就是说即使收到测量数据但是还是不确飞机位置在哪。于是我得需要根据前一个时刻的位置估计出当前时刻的飞机位置 结合 测量数据 综合考虑来 估计当前飞机位置。这就是卡尔曼滤波的作用。
那么你一定会问根据前一个时刻估计的飞机位置怎么就可以估计现在这个时刻的飞机位置了?
答:卡尔曼认为所有的状态变化(位置变化)都是线性的。什么叫做线性?上个时刻位置是0.3,速度是0.2。那么我估计下个时刻的位置就是0.5。这就叫做线性。
接下来你一定会问那并不是所有的状态变化都是线性的怎么办?
你像风速变化它就不是线性的。
答:恭喜你发明了新的算法。事实上别人已经为这个算法命名了叫做扩展卡尔曼滤波。现在我们要学习的是卡尔曼滤波。你只需要记住卡尔曼滤波就是认为所有变化都是线性的。
那么现在我知道了怎么用上个时刻飞机的位置估计当前时刻的飞机位置,也知道了还得借助当前时刻收到的测量数据来综合考虑来估计当前飞机的位置。那么怎么综合考虑呢?这就涉及到一个比例。到底这两个数据占比多少?这就是卡尔曼滤波的核心精髓。卡尔曼滤波算法要动态的调这个比例。
滤波算法的思路发展
如果不理解滤波思路那么今天学会了一个卡尔曼滤波明天还有一个通尔曼滤波要你学。如果学会这些滤波算法的思路,把他们联系在一起然后记忆那就简单多了。滤波算法本质上就是利用多个数据来融合估计真实状态。下面举两个从浅到深的例子。
下面有个一个飞机只会水平飞行。我们已知上个时刻飞机的位置x1 和速度v1 而且雷达可以测量到t2 此时飞机的位置x_2^* 。那么我们估计飞机的位置那就有两种方法:一是认为飞机是匀速(v2 = v1) 直线运动得到现在飞机位置为x1 + v2 ( t 2 − t 1 ) ,另一种是认为飞机位置就是测量值x_2^*t 。如果按第一种那么万一飞机不是匀速走呢?如果按第二种万一雷达很不准呢?因此得采取一种折中的方法。
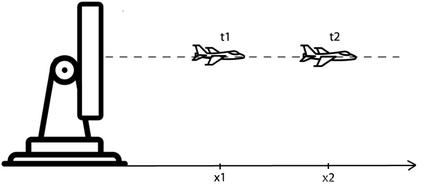
我们认为飞机在时刻t_2的位置为
这个α 需要我们自己设置。如果我们相信雷达不准那就α 赋值很低比如为0.1.如果我们相信雷达很准那么就设置α x为很接近1的值比如0.9。你会发现α x越接近0,那么所估计的位置越是接近认为飞机匀速走的那个思路。越接近1那么所估计的位置越接近雷达测量值(等于1就是认为飞机在时刻t2的位置就是雷达测量值)。
但是飞机的速度怎么估计啊?因为飞机不一定是匀速走。
速度估计的方式有两种:
- 假设飞机是匀速运动。也就是说t1 到t2 这段时间内飞机速度等于在t1 时刻估计出的飞机速度v1。即v2 = v1 。
- 由于雷达也收到了一个测量数据,它测量到雷达距离飞机位置是x 2 ∗ x_2^x 。也就是说在雷达看来从t1到t2 这段时间内飞机走过了x_2^ − x1 这么远的距离。所以根据雷达的判断,我们可以估计出飞机的一个速度
 这两种速度很可能不同。这有两个原因:“一是飞机并不是匀速运动,二是雷达根本就测量的距离不准”。到底是哪个对呢?
这两种速度很可能不同。这有两个原因:“一是飞机并不是匀速运动,二是雷达根本就测量的距离不准”。到底是哪个对呢?
真实速度需要综合考虑这两个数值,根据上一个例子总结的滤波器模式第N次算出的估计值=上次的估计值+ 因子a ×(测量值-上次估计值)。我们知道真实的速度肯定可以这么表达 至于这个β 到底取多少这是我们自己赋值。比如我们觉得测量的值是更准确的,那β 可以设置大一点比如0.9。如果我们觉得雷达不准那就β设置小一点比如0.1。
至于这个β 到底取多少这是我们自己赋值。比如我们觉得测量的值是更准确的,那β 可以设置大一点比如0.9。如果我们觉得雷达不准那就β设置小一点比如0.1。
所以我们得到速度的估计公式:
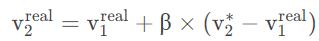
然后我们又可以根据这个求得的速度来更精确的估计飞机的位置

如何结合“飞机的速度,加速度,雷达测量的飞机的位置” 来估计飞机的位置?
在前面我们一直做的假设是飞机是匀速走的。但是飞机很可能会发生加速或者减速。这就不得不考虑加速度的问题了。
在高中我们学过位移与速度和加速度之间的关系是:

其中a2是从t1到t2这段时间的加速度。
所以飞机的位置可以融合速度、加速度这样来估计:


可以看到和前面那个例子的位置估计公式:
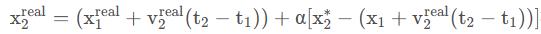
相比,只是将原来的根据速度估计位移变成了根据速度和加速度来估计位移。
在前面提到了我们的速度可以根据测量数进行动态更新:

当然我们的加速度也是可以根据测量数据进行动态更新的
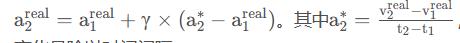
这个是根据加速度的定义所得来的,加速度=速度变化量除以时间间隔。
可以看到滤波思路是一环扣一环,它要平衡每个环节中的 根据之前状态所估计出当前状态值 和 测量值之间的在最终结果中的占比。
而那些滤波算法要做的事就是设计合理的占比到底取多少比较合适。而且是需要根据不同情况动态的设置占比。前面提到的例子中占比变量有三个α , β , γ 你学习滤波算法时只需要关注这几个占比值是怎么计算的就可以了。
像卡尔曼滤波,拓展的卡尔曼滤波,Particle Filter,贝叶斯滤波等等都是前面提到滤波思路这种形式。
卡尔曼滤波滤波步骤
- 估计当前时刻位置

- 估计当前时刻速度:

- 估计当前时刻加速度:
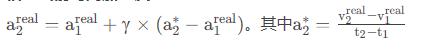
前面我们提到了那些种类繁多的滤波算法,无非就是提出了各种确定α , β , γ具体取值的计算方法而已。
我们看看卡尔曼滤波是怎么确定这三个值的。
- α这个是用来调节 根据上个位置估计出的当前位置值 与 测量值 在最终结果中的占比用的。这个在卡尔曼滤波中叫做卡尔曼增益。当然既然叫卡尔曼增益了肯定变量名就不叫做α 了而是叫做Kn
- β 是用来调节根据上个时刻速度估计出的当前时刻速度值 与 根据测量值算出的速度 在最终结果中的这两个数占比用的。在卡尔曼滤波中它认为物体就是匀速运动的。所以当前时刻速度和上个时刻速度一样,即β=0。
- 上面那句话提到了物体是匀速运动的所以没有加速度。
于是卡尔曼滤波可以这么写:
- 估计当前时刻位置:

- 估计当前时刻速度:

那么Kn怎么计算呢

橘黄色虚线是根据市上个状态计算出当前状态的估计值,绿色虚线是测量值,紫色虚线是最终结果。而Kn这个数字就是调节紫色虚线到底是靠近另外两条线中的哪个。

现在我们得到了新的位置估计值,那么根据这个来估计下一个位置它的方差Pn-1是多少呢?由于根据上个状态算出当前状态这个数字在最终结果的占比只占了1 - Kn,所以方差Pn=(1-kn)Pn-1
由上面这段话可以看出,卡尔曼滤波最关键的是需要求出两种方差。一是纯粹依赖估计的这种方法的方差。二是测量仪器的方差。只要知道了这两个值那就可以知道估计值和测量值在最终结果中的占比。算方差的方法在不同应用场景是不同的需要以实际情况而定。
注意:根据上个状态估计当前时刻的位置方法不是只有根据速度和加速度来估计这一种方法。还有其他很多种。比如我可以根据飞机发动机此时的推动力和这段时间内燃烧了的汽油来估计飞机飞行了的距离(能量守恒定律,推动力×距离=做功)。
Python编程实践卡尔曼滤波
"""
@司南牧
"""
import numpy as np
# 模拟数据
t = np.linspace(1,100,100)
a = 0.5
position = (a * t**2)/2
position_noise = position+np.random.normal(0,120,size=(t.shape[0]))
import matplotlib.pyplot as plt
plt.plot(t,position,label='truth position')
plt.plot(t,position_noise,label='only use measured position')
# 初试的估计导弹的位置就直接用GPS测量的位置
predicts = [position_noise[0]]
position_predict = predicts[0]
predict_var = 0
odo_var = 120**2 #这是我们自己设定的位置测量仪器的方差,越大则测量值占比越低
v_std = 50 # 测量仪器的方差
for i in range(1,t.shape[0]):
dv = (position[i]-position[i-1]) + np.random.normal(0,50) # 模拟从IMU读取出的速度
position_predict = position_predict + dv # 利用上个时刻的位置和速度预测当前位置
predict_var += v_std**2 # 更新预测数据的方差
# 下面是Kalman滤波
position_predict = position_predict*odo_var/(predict_var + odo_var)+position_noise[i]*predict_var/(predict_var + odo_var)
predict_var = (predict_var * odo_var)/(predict_var + odo_var)**2
predicts.append(position_predict)
plt.plot(t,predicts,label='kalman filtered position')
plt.legend()
plt.show()

雷达的主要用途可以大致分为
- 检测
- 跟踪
- 成像。
信号获取和干扰抑制也是实现这些功能的必要技术,雷达最为基本的用途是对一类物体或者物理现象进行检测。这就需要确定在某一给定时 $\scriptstyle{d(t)}$ 刻接收机的输出究竟是一个反射体的回波,还是只有噪声。
通常会将接收机输出的幅度A(t) (t表示时间)与二个阈值T(t)进行比较,以检测判决。这个阈值可以在雷达设计时根据系统情况预先确定,也可以根据雷达回波数据自适应计算得到,将会解释这种检测技术的合理性。当一个脉冲传播到距离 $R$ 处后返回,其总的传播路径长度为2R,所需要的时间就是2R/c , ,则可以认为在距离 R 处存在一个目标,该这样如果在脉冲发射后的某一时刻
$$
R={\frac{c t_{0}}{2}}
$$
其中c为光速
一旦雷达监测到了一个目标,则希望对他的速度进行跟踪。
单基雷达的特点决定了其位置测量是在一个球坐标系内完成的。
该坐标系的原点就是雷达的相位中心。
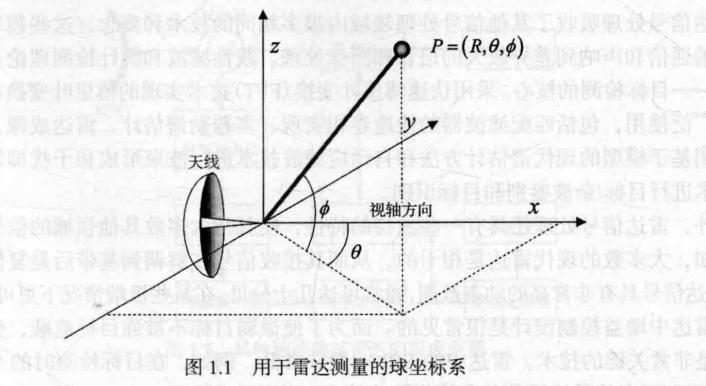
规定天线指向的方向就是坐标系的+x方向。
角度θ为方位角,角Φ为俯仰角,距离为R
这三个参数即目标在该球坐标系内的位置。
对于目标速度,需要测雷达回波的多普勒频移。
对于单基雷达仅能测模板的径向速度。
在跟踪功能中,基本的性能指标是距离、角度、速度估计的精度。虽然分辨率可以作为跟踪精度的一个粗略的上界,但通过适当的信号处理后,雷达可以获得的精度最终取决于具体的SIR。
在成像中,最基本的指标是空间分辨率和动态范围。空间分辨率决定着在最终的合成孔径雷达(SAR)图像中多大尺寸的物体可以被辨识出来,进而决定该雷达图像的应用范围。例如,分辨率1kmx1km的图像可以用于对陆地使用情况的研究,却不能用于对机场和导弹阵地的军事监视。动态范围决定着图像的对比度,也决定了从一幅图像中能提取的信息量。
雷达信号处理的目的就是提高这些指标。通过脉冲积累可以提高雷达信号的SIR。通过脉冲压缩和其他波形设计技术(如频率捷变)可以同时改善雷达的分辨率和 SIR。增大SIR和采用插值技术可以提高测量的精度。在信号处理中广泛使用的加窗技术同样可以改善雷达的旁瓣特性。这些问题都将在后续几章中讨论。
** 雷达的指标参数**
| 参数名称 | 描述 |
|---|---|
| $P_d$ | 检测概率 |
| $P_{FA}$ | 虚报概率 |
| SIR | 信干比 |
| 分辨率 | |
| 旁瓣特性 | |
| 跟踪距离 | |
| 跟踪角度 | |
| 速度估计 |
单脉冲雷达体系
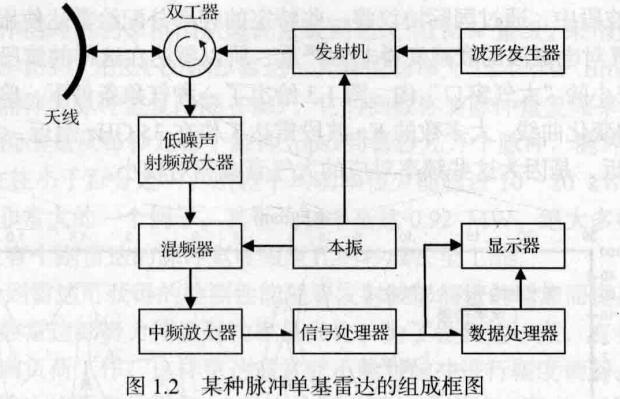
图所示的脉冲单基雷达的结构并不是唯一的。例如,很多雷达系统在中频而非基带完成某些信号处理功能,在中频完成的常见的信号处理功能包括:匹配滤波、脉冲压缩、某种类型的多普勒滤波,等等。这些信号处理功能本身也是有重复的,例如脉冲压缩和多普勒滤波都可以看成匹配滤波的一部分。
不同雷达系统的结构区别还包括雷达系统是在哪一点将模拟信号数字化的。早期的雷达系统是全模拟的,而现在很多雷达是在信号转换到基带之后进行数字化的。对于这类雷达,任何在中频进行的信号处理都是依靠模拟技术完成的。目前越来越多的新的雷达设计在中频就对信号进行数字化,这样A/D变换就更加靠近雷达的前端也使得在中频就可以采用数字信号处理技术。最后需要说明的是,信号处理和数据处理的界限有时是不清楚的,或者人为规定的。
在下面 将简要介绍雷达基本子系统的主要特点
发射机和波形产生器
发射机和波形产生器对于确定雷达的灵敏度和距离分辨率是非常重要的。目前雷达系统已经使用的工作频率最低低至2MHz,最高高至220GHz。
激光雷达的工作频率在10^12 ~ 10^15Hz的量级,对应波长0.330um。然而,大多数的雷达工作在微波波段,其频率范围为200MHz95GHz对应波长0.67m 3.16mm。
表11列举了用字母缩写命名的常见的雷达波段(IEEE,1976)。其中毫米波波段有时进一步划分为子波段3646GHz为Q波段4656GHz为V波段56~100GHz为W波段(Richards等,2010)。

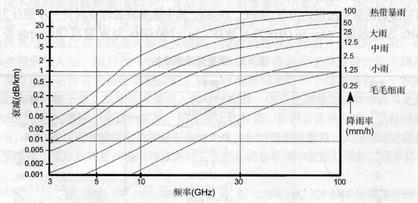
在HF到Ka 波段中,通过国际协议将一些特定的频率分配给雷达使用。另外,在频率高于X波段时,大气对电磁波的衰减变得非常严重,所以雷达在这样的波段工作时,通常工作在大气衰减相对较小的“大气窗口”内。图1.3给出了一种气象条件下单程传播的大气衰减随雷达工作频率的变化曲线。大多数的Ka波段雷达工作在35GHZ附近大多数W波段雷达工作在95GHz附近,是因为这些频率对应的大气衰减相对较小。
对较远距离进行探测时,人们倾向于使用较低的雷达频率,其原因在于较低频率能够获得较低的大气衰减和较大的功率。对近距离进行较高分辨率的探测,人们倾向于使用较高的雷达频率,是因为在给定天线尺寸的情况下,较高频率可以得到较窄的波束宽度,同时较高
的频率也带来了较大的大气衰减和较低的可用功率。
天气条件对于雷达的信号传播也有比较显著的影响。图 1.4给出了降雨率从毛毛细雨到倾盆大雨各种条件下,信号传播的单程损失随射频频率的变化曲线。X 波段频率(10GHZ的典型情况)和更低的频率只有在大雨情况下才受到明显影响,而毫米波波段即使在小到中等雨量的情况下也会受到非常大的衰减。
雷达发射机工作的峰值功率范围从毫瓦量级到超过 10MW量级。采用更大功率发射机的一个例子是AN/FPS-108 COBRADANE雷达,其峰值功率为15.4MW(Brookner,1988)。人们将脉冲之间的间隔称为脉冲重复间隔(PRI),它的倒数称为脉冲重复频率(PRF)。PRF的范围也很宽,通常的范围是从每秒几百个脉冲(pps)到每秒几万个脉冲。脉冲系统的工作比(占空比)通常较低,往往小于百分之一,所以平均功率很少能超过 10~20 W。COBRA DANE雷达也是平均功率非常大的一个例子,其平均功率高达0.92MW。绝大多数雷达脉冲宽度为100ns~100us,也有个别雷达的脉冲宽度短至几纳秒或长至1ms。
雷达可获得的检测性能随着发射波形能量的增加而提高。为了获得最大的检测距离,大多数雷达都努力使发射功率最大化。为了做到这一点,有种方法是在脉冲工作期间总让发射机满负荷工作,这样雷达通常就不能对脉冲进行幅度调制。雷达的距离分辨率ΔR是由波形带宽β决定的,即

对于一个没有调制的脉冲,其带宽反比于时宽。对于给定的脉冲宽度,为了在增加波形带宽的同时不损失能量,很多雷达通常采用对脉冲进行相位调制或频率调制的方法。
距离分辨率的数值与雷达功能有关,在远程监视雷达系统中距离分辨率可以差到几千米此时倾向于采用较低的射频频率,而在高分辨成像系统中,距离分辨率往往精细至1m甚至更小。相应的波形带宽的数量级为100 kHz~1GH典型情况下小于射频频率的1%,个别雷达能够达到射频频率的 10%。所以大多数雷达的波形可以看成窄带的带通函数。
天线
天线对于确定雷达的灵敏度和角度分辨率是非常重要的。雷达系统可以采用的天线类型是多种多样的。常见的类型包括抛物面反射天线、扫描馈源天线、透镜天线和相控阵天线。从信号处理的角度,天线最重要的特性是增益、波束宽度和旁瓣电平。这些特性都是从天线的功率方向图得到的。
功率方向图$P(\theta,\phi)$描述了发射过程中天线对$(\theta,\phi)$方向的辐射强度$(\theta,\phi)$是以达的瞄准线方向为参考方向定义的。对于归一化方向图,撇开不重要的比例因子功率方向图和辐射的电场强度 $E(\theta,\phi)$是密切相关的,$E(\theta,\phi)$称为天线电压方向图,对应关系为
$$P(\theta,\phi)=|E(\theta,\phi)|^2$$

对于大多数工作情况只关心其远场(也称Fraunhofer)功率方向图。若天线的孔径为D,通常定义的远场起始距离为$D^2/\lambda$或$2D^2/\lambda$。考虑如图1.5所示的一维线孔径的方位方向图。从信号处理的观点,孔径天线(如平面阵和反射抛物面)的重要特性是,远场的电场强度随方位角变化的函数E(θ)是方位孔径上电流分布A(y)的傅里叶变换(Bracewell,1999;Skolnik,2001),即

其中,频率变量为(2*Π/λ)sin0,频率变量的单位为 rad/m。
为了使上述关系更加清楚,定义s=sin0,=y/λ,可得

零中频采样
零中频采样过程如图所示:

假设信号为:

为了计算简便,所有的频率中省略2 π 2\pi2π以及相位。
对这个信号进行零中频正交采样,得到:

过低通滤波器之后,变为:
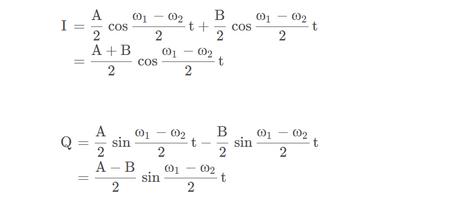
这样就将信号降至零中频,也就是基带。这时,信号带宽为射频带宽的一半,即B/2 。因此,可以用f_s = B
信号重构
零中频采样之后信号的重构过程如图所示:

以上面的零中频采样之后的信号为例。分别乘以同相和正交的频率之后,得到:

最后两路信号相加:


关于博主
an actually real engineer
通信工程专业毕业,7年开发经验
技术栈:
精通c/c++
精通golang
熟悉常见的脚本,js,lua,python,php
熟悉电路基础,嵌入式,单片机
耕耘领域:
服务端开发
嵌入式开发
>gin接口代码CURD生成工具
sql ddl to struct and markdown,将sql表自动化生成代码内对应的结构体和markdown表格格式,节省宝贵的时间。
qt .ui文件转css文件
duilib xml 自动生成绑定控件代码
协议调试器
基于lua虚拟机的的协议调试器软件 支持的协议有:
串口
tcp客户端/服务端
udp 组播/udp节点
tcp websocket 客户端/服务端
软件界面

使用例子: 通过脚本来获得接收到的数据并写入文件和展示在界面上
下载地址和源码
webrtc easy demo
webrtc c++ native 库 demo 实现功能:
基于QT
webrtc摄像头/桌面捕获功能
opengl渲染/多播放窗格管理
janus meeting room
下载地址和源码
wifi,蓝牙 - 无线开关
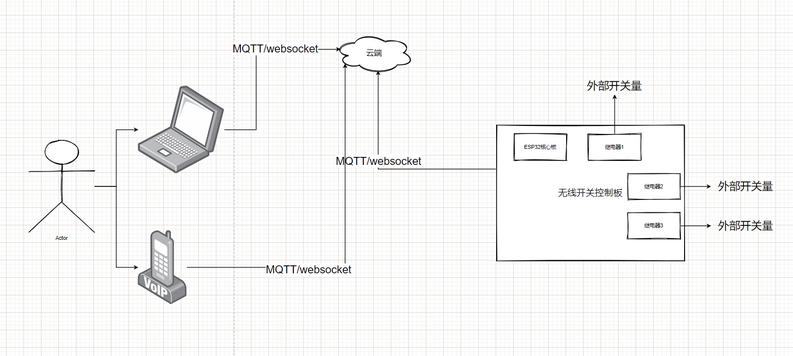
实现功能:
通过wifi/蓝牙实现远程开关电器或者其他电子设备
电路原理图:
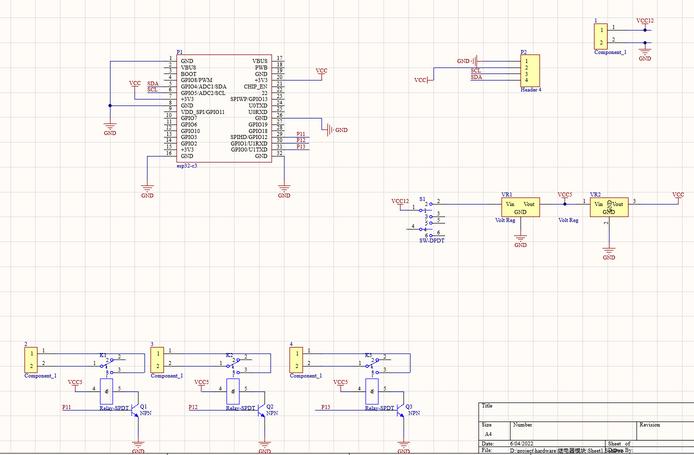
实物图:

深度学习验证工具
虚拟示波器
硬件实物图:

实现原理
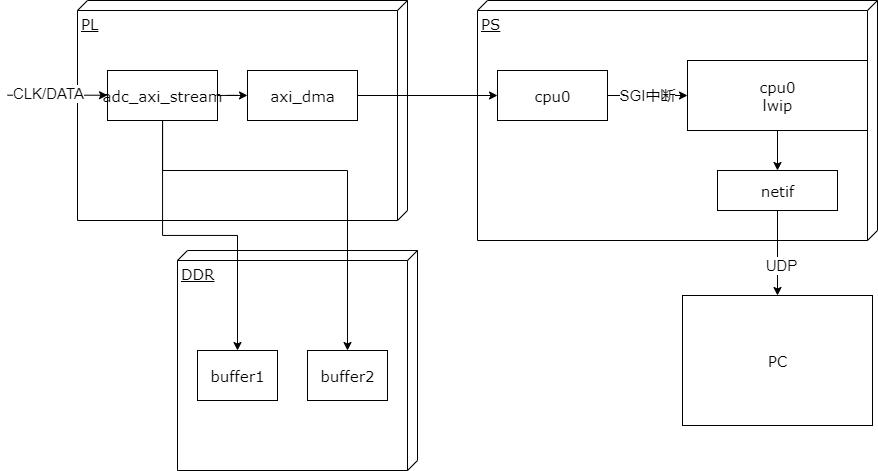
基本性能
采集频率: 取决于外部adc模块和ebaz4205矿板的以太网接口速率,最高可以达到100M/8 约为12.5MPS
上位机实现功能: 采集,显示波形,存储wave文件。
参数可运行时配置
上位机:

显示缓冲区大小可调
刷新率可调节
触发显示刷新可调节
又一个modbus调试工具
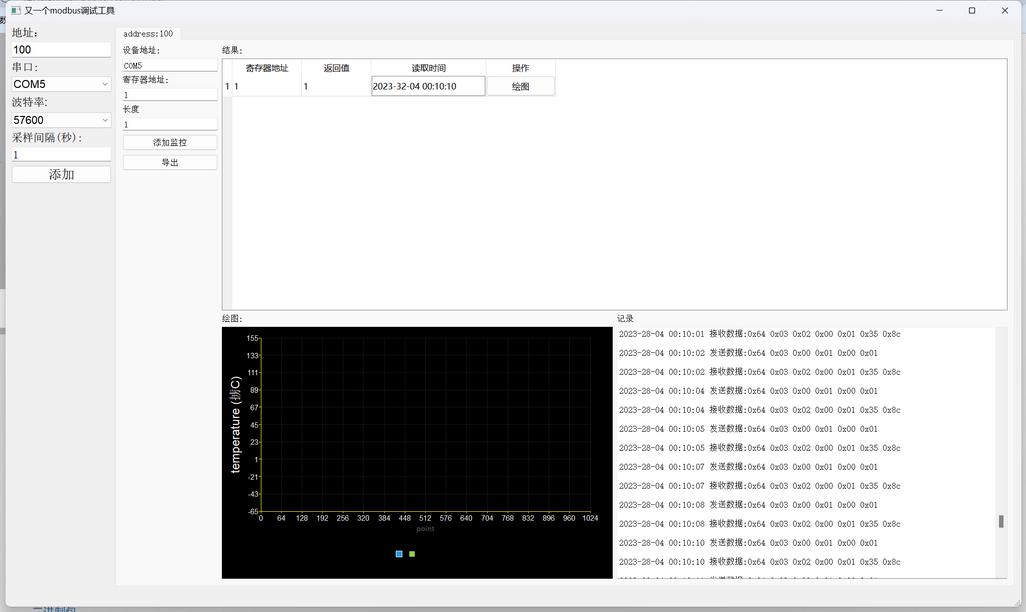
最近混迹物联网企业,发现目前缺少一个简易可用的modbus调试工具,本软件旨在为开发者提供一个简单modbus测试工具。
主打一个代码简单易修改。
特点:
1. 基于QT5
2. 基于libmodbus
3. 三方库完全跨平台,linux/windows。
开源plutosdr 板卡

1. 完全开源
2. 提高固件定制服务
3. 硬件售价450 手焊产量有线
测试数据
内部DDS回环测试

接收测试
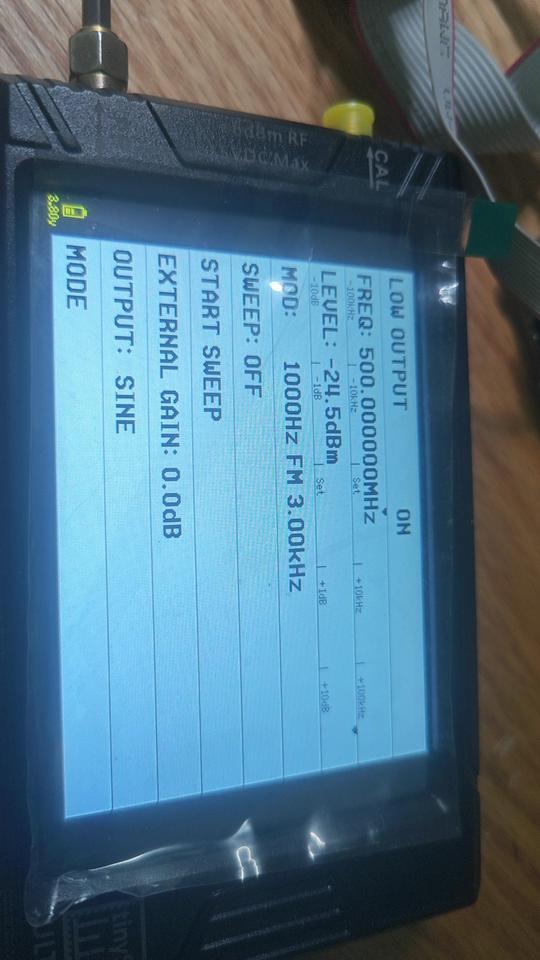
外部发送500MHZ FM波形
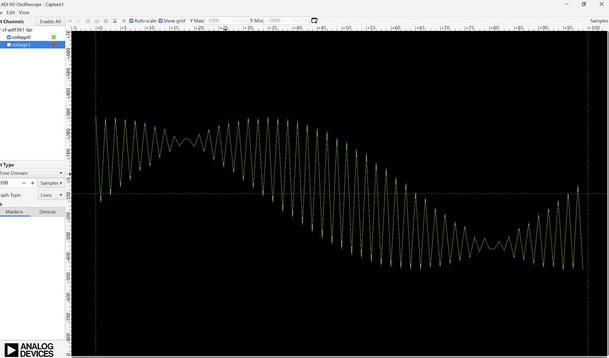
matlab测试

2TRX版本

大部分plutosdr应用场景都是讲plutosdr板卡作为射频收发器来使用。
实际上plutosdr板卡本身运行linux 操作系统。是具有一定脱机运算的能力。
对于一些微型频谱检测,简单射频信号收发等应用完全可以将应用层直接实现在板卡上
相较于通过网卡或者USB口传输具有更稳定,带宽更高等优点。
本开源板卡由于了SD卡启动,较原版pluto支持了自定义启动应用的功能。
提供了应用层开发SDK(编译器,buildroot文件系统)。
通过usb连接电脑,经过RNDIS驱动可以近似为通过网卡连接
(支持固件的开发定制)。
二次开发例子
```
all:
arm-linux-gnueabihf-gcc -mfloat-abi=hard --sysroot=/root/v0.32_2trx/buildroot/output/staging -std=gnu99 -g -o pluto_stream ad9361-iiostream.c -lpthread -liio -lm -Wall -Wextra -lrt
clean:
rm pluto_stream
版面分析即分析出图片内的具体文件元素,如文档标题,文档内容,文档页码等,本工具基于cnstd模型