频域分析与设计法 是
经典控制理论的 核心内容 。频域法中用到的Bode plot,Nyquist plot等是工程中控制设计与分析有力的工具。学好频域法是学好经典控制内容最重要的一步。
应当认识到现代控制技术多已经转向以
状态空间分析法为主的时域分析方法,但是频域分析方法在实际工程中依旧能够提供丰富的信息。这其中不乏很多信号分析的有关知识和技巧,涉及到“
信号与系统(Signals & Systems)”与“
数字信号处理(Digtial Signal Processing,DSP)”等方面。
我们之前讲过
时域分析系统性能和根轨迹设计。在频域分析与设计中,我们同样有频域中的系统性能指标,以及设计相应指标的设计方法。在
频域中,利用Bode plot和Nyquist plot等图解方法可以高效地完成SISO系统的设计工作。
本篇介绍频域分析方法一些基础,为后续做铺垫:
1. 频率响应 Frequency Response
频率响应(Frequency Response)通常是指LTI系统对正弦类信号的响应。如果LTI系统是稳定的,当瞬态消失后,最后响应只留下的稳态信号依旧是正弦类信号,只是幅值和相位发生了改变。我们发现当一个传递函数为 $G(s)$ 的系统输入正弦类函数后,其幅值会变为原来的 $|G(j\omega)|$ 倍,
相位差变成了 $\angle{G(j\omega)}$ ,这样我们可以把幅频特性和相频特性用幂指数的方法结合在一起 $G(j\omega )=\left| G(j\omega ) \right|{{e}^{j\angle G(j\omega )}}\text{=}A(\omega ){{e}^{j\varphi (\omega )}}$ 。这一点在
非线性系统或者时变系统中 不成立 ,输出的信号最后可能含有除了输入信号频率之外的频率。我们把 $A(\omega)$ 称为幅值频率特性(magnitude), $\varphi(\omega)$ 称为相位频率特性(phase)。
2. 伯德图 Bode Plot
伯德图 (Bode Plot) 是频域分析的重要工具,它图示了系统的频率特性。
Bode Plot 由对数幅频曲线和对数相频曲线组成。在Bode Plot中频率特性 $G(j\omega)$ 可以根据对数的性质分解成独立乘积项的对数之和差。一般纵轴上的幅值会以分贝(dB)为单位。由于Power dB的标准定义式是功率之比的以10为底的对数的十倍:
$|G{{|}{db}}=10{{\log }{10}}\frac{{{P}{2}}}{{{P}{1}}} \$
我们知道功率与电压的平方成正比,所以功率增益power gain也可以写作
$|G{{|}{db}}=20{{\log }{10}}\frac{{{V}{2}}}{{{V}{1}}} \$
这就是Bode图中纵轴幅值以 $20\log_{10}{(\cdot)}$ 形式出现的原因,此外幅值的乘除由于对数的性质就可以转化为加减运算,方便了Bode图曲线的叠加。
Bode的横轴采用的对数分度,当频率增大10倍时,坐标轴上距离变化为一个单位长度。这种做法使横轴实现了非线性的压缩,能够在较大频率范围内表示频率特性的变化[2]。
频域设计法和根轨迹设计法中设计
闭环控制系统的思路是一样的,即 通过系统开环传递函数来设计对应的闭环系统指标,达到设计要求 。所以应该明确一般设计控制器时,我们都会根据 开环传递函数(Open loop transfer function,OLTF) 来画 开环Bode plot 。我们会在接下来的几篇文章中介绍开环Bode plot设计方法。
设计开环Bode plot的意义在于我们可以 不断调整开环传递函数(OLTF) ,其中包含了我们想要设计的控制器或者补偿器部分, 来实现达到闭环设计指标的目的。 可以对比我们在根轨迹设计中的做法,我们同样是根据开环传递函数画出了闭环系统的根轨迹来确定系统性能的。 至于如何调整OLTF,我们会在接下来介绍****
相位裕度(phase margin,PM),幅值裕度(gain margin,GM),
穿越频率**(crossover frequency)**等开环频域指标以及他们是如何影响闭环系统性能的。
我们也可以画 闭环Bode plot。 闭环Bode plot是闭环系统在频域中幅值与相位的图示。这与时域中闭环系统的
响应曲线表示系统性能的意义是一致的,即闭环Bode plot中我们也可以定义闭环频域指标,我们将闭环频域指标与闭环时域指标进行对应。所以时域指标就可以转化为频域指标,通过频域设计的方法实现。关于开环Bode plot和闭环Bode plot的内容,我认为
的回答非常好,以下贴链接:
开环或者闭环传递函数的伯德图意义?561 赞同 · 23 评论回答
总结一下Bode plot设计闭环控制系统的思路:
设计controller(or compensator) $D_c(s)$ → 画出
开环传递函数 $D_c(s)G(s)H(s)$ 的Bode plot → 根据开环频域指标调整设计 → 画出闭环传递函数的Bode plot → 检验各闭环指标
3. 带宽 Bandwidth
频率特性本身并没有要求一定要是
开环系统或者闭环系统的特性。 即便如此,我们最后关心的还是 闭环系统的频率特性 ,因为我们最终的目的就是要设计控制器来实现闭环控制,让闭环系统达到我们期望的性能。因此 建立起闭环频率特性与系统性能之间的联系是很有必要的,这将指导我们检验频域设计的好坏 。 研究开环频率特性便于我们进行控制器设计,最终目的还是要让闭环频率特性达到我们的要求。
带宽 (Bandwidth)是闭环系统的一个设计指标之一。以机械系统中典型的二阶标准系统为例:
$G(s)=\frac{1}{(s/\omega_n)^2+2\zeta(s/\omega_n)+1} \$
其Bode plot如下,横轴这里取的是与
自然频率的比值:
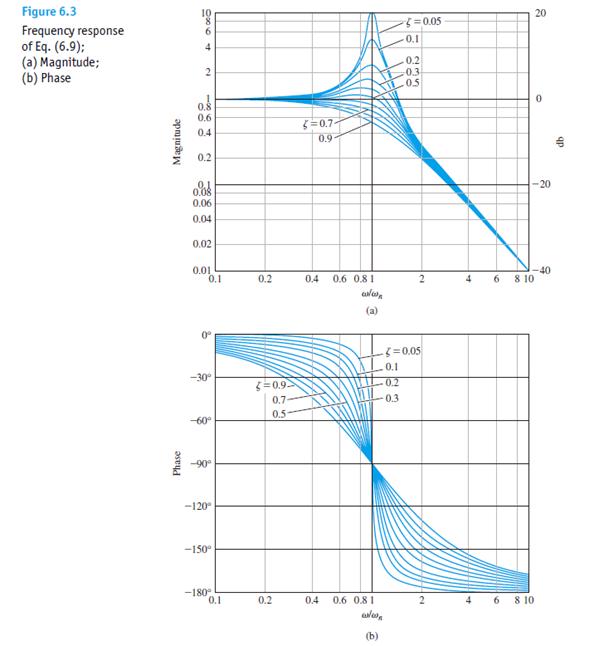
我们定义带宽是幅值第一次衰减到比DC gain小-3db的值或者DC gain的70.7%处时的频率。这个点的来源是由于此时系统的稳态输出的功率变为了原来的1/2,所以幅值就是原来的 $\sqrt{1/2}$ ,即0.707。对于图示的系统,由于DC gain为1(即s=0时稳态输出与输入幅值比为1),所以带宽频率就对应幅值为-3db处的频率。在带宽频率之内我们认为系统的输出还是能够很好的跟踪正弦输入的,超出带宽之外我们发现幅值随着频率会骤然下降。低通滤波器的
截止频率(Cutoff frequency)和这里的带宽定义式一致的。
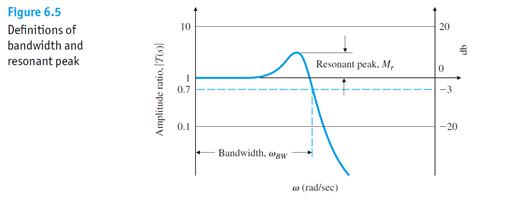
Bandwidth是一个很重要的用来衡量响应速度的指标,非常类似于时域中的rise time或者peak time。图6.3中
阻尼比0.7左右时,带宽和自然频率基本相等,从而可以用带宽来替代自然频率估计系统性能,在其他阻尼比时也可以近似这样处理。
需要指出的是这里对Bandwidth的定义是基于有低通滤波器(low-pass filter)性质的系统而言的,也就是说在低频率时(s较小时)输出的幅值比能保持为一个较大的数值, 从而实现低频率信号“直接”通过的目的,即低通的含义。从6.3和6.5中我们都能看出,随着频率变高,信号衰减越来越厉害,做到了“阻止”高频信号通过,即高阻。 低通高阻是low-pass filter的特点,绝大部分实际的控制系统都是如此的。 回忆我们说过绝大多数的实际系统的传递函数都是proper的,也就是分子阶次低于分母阶次。
我们以 $G=\frac{s+1}{s^2+0.5s+4}$ 为例,这个传递函数的DC gain是s=0时的值,为1/4。随着s的增大,这个传递函数趋于0,在bode plot上就会不断下降。因此我们可以想象其频率特性曲线的样子。 下图是MATLAB中用bode命令绘画出来的图。
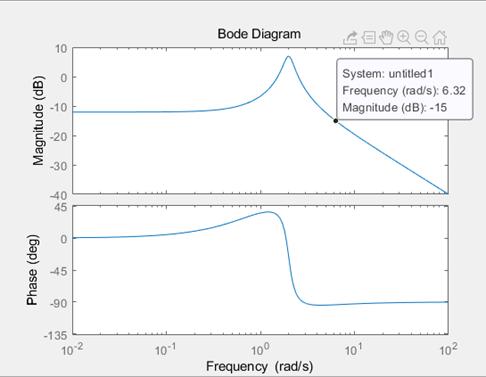
我们看到Bode Plot在频率很小时,其幅值为 -12 dB左右,正是20log(1/4)的值(-12.0412)。在一段频率区间之内其幅频一直保持不变,随后迎来了共振峰,然后会开始下降。这与我们的预期分析是一致的。我们可以计算带宽的大小,应该是在幅频为-12db-3db=-15dB处的频率。我们可以看到约为6.32就是我们知道的带宽。带宽越大,这个系统响应速度就越快,我们在下一篇文章中讲Bode Plot的绘制时再提一提这个理解。
那么如果分子和分母的阶次一样了会怎么样呢,我们可以想象其频率不断增大时,其输出幅值会保持在一个数。例如一个一阶高通滤波器(High-pass filter)
$G=\frac{s}{s+1} \$
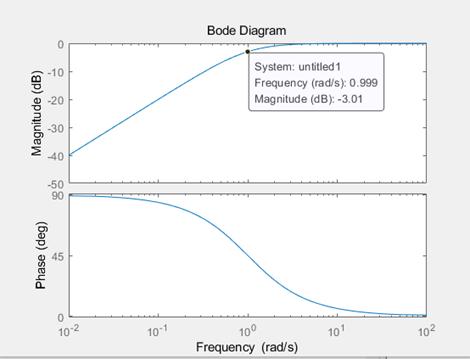
这个HPF的截止频率同样一般是定义为0dB-3dB=-3dB处的频率,也就是极点s=-1处。但是我们却无法定义其带宽,因为随着s增大,其值只会慢慢接近0dB,也可以认为其带宽是无穷大的,输出会和输入的幅值相等,实现“高通低阻”。
对于一般的系统基本都是具有低阶滤波器性质的,频率不断增加信号会衰减,因此分母的阶次都会比分子要高,这与Bode Plot所显示的高频部分是对应的。
带宽的定义并不是唯一的,我们可以自己定义cutoff frequency,但是在控制工程中一般还是以-3dB为标准。
关于传递函数阶数的问题可以参考知乎回答,希望给大家一点启示:
为什么传递函数分母中s的阶数n必不小于分子中s的阶数m?63 赞同 · 19 评论回答
**4. 系统型号System Type 与 **
稳态误差** Steady-state Error**
我们再一次回到了System Type和稳态误差的问题。
我们重新回顾一下,我们这里的稳态误差是指系统对多项式信号(Polynomial Signal)的稳态误差。你可能注意到了一个问题,频率特性的幅频特性其实也是一种稳态误差的表现。在不同频率下,输入信号与输出信号的比值会发生变化。对于实际系统我们发现随着频率的增加,输出信号的幅值会越来越小,这意味着正弦类信号的稳态误差会随着频率的增大而逐渐增大,误差的最大值应该会逼近原输入信号的幅值(因为幅频随着频率会趋于无穷小)。
我们先以0型系统为例,依旧是 $G=\frac{s+1}{{{s}^{2}}+0.5s+4}$ 。其Bode Plot我们在上面已经画过了。
我们分析得到,当频率非常小时,原频率特性直流增益 $\underset{\omega \to 0}{\mathop{\lim }},G(j\omega )=\underset{\omega \to 0}{\mathop{\lim }},\frac{j\omega +1}{-{{\omega }^{2}}+0.5j\omega +4}=1/4 \$
我们之间计算过0型系统对
阶跃信号step input的稳态误差,单位反馈时为
$[{{e}_{ss}}=\underset{s\to 0}{\mathop{\lim }},\frac{1}{1+G(s)}=\underset{\omega \to 0}{\mathop{\lim }},\frac{1}{1+G(j\omega )}=\frac{1}{1+G(0)}]$
由此我们发现大的DC gain可以减小闭环系统的稳态误差。在单位反馈(unity feedback)时,DC gain就是该系统的位置误差系数。并且我们发现0型系统的bode plot在低频段是近似一条斜率为0的直线,和常数一样。确实,低频段我们发现幅频值与DC gain几乎一样。
由此我们可以推广到一个n型系统,其开环传递函数中有n个积分器(1/s)。对应的频率特性在低频段我们可以得到一个近似的结果:
$[G(j\omega )=K(j\omega )\cdot {{(j\omega )}^{-n}}\cong K(0)\cdot {{(j\omega )}^{-n}}={{K}_{0}}\cdot {{(j\omega )}^{-n}}]$
上面这个结果需要你动手写一写,看看能不能得到。
当n=0时,0型系统的低频曲线为常数 $K_0$ ,即DC gain。
当n=1时,I型系统的低频曲线为 ${{K}{0}}\cdot {{(\omega )}^{-1}}\text{=}\frac{{{K}{0}}}{\omega }$ 。我们将这个幅值化为分贝dB,低频曲线方程约为 $[y=20{{\log }{10}}{{K}{0}}-20{{\log }_{10}}\omega ]$ ,可知曲线以-20dB/decade下降 。当 $\omega=1$ 时我们就可以从图中读出 $K_0$ 的值。 $K_0$ 是除去一个积分器后开环函数的DC gain。
下图是 $G(\text{s})=\frac{2}{s(s+5)}$ 的Bode Plot,可以验证此时实际的 $K_0$ 为0.4(-7.96dB),斜率为-20dB/decade。根据上面的结论 $\omega=1$ 时我们得到 $K_0$ 约为-8.14,结果是很接近的。
更高type的系统同理,曲线斜率会增大,每提高一个type,就会增加-20db/decade的斜率,其除去积分器后开环函数的DC gain总是可以从图中找出。我们在后续设计中总希望这个常数能够增大一些,让稳态误差减小。
本篇小节:
这篇先对频域设计和分析方法有一个大概介绍,并且简单回顾了频率特性和Bode Plot的概念,重点提了提Bandwidth和Steady-state error。我按照 [1]里的顺序对这块进行总结和重点分析,我觉得总体上是非常合理的,也给学习[2]的同学一点不一样的感觉。
下一篇文章会讲Bode Plot的绘制,我觉得相比于
根轨迹的绘制,Bode Plot的绘制方法对理解Bode Plot是很大帮助的。Bode Plot对系统的
频率特性进行了图示,让我们一目了然地看清了系统在不同频率下的幅值与相位的变化。我们可以对某一个系统的低频响应和高频响应做出判断。我们以低通滤波器LPF和高通滤波器HPF为例,画了它们各自的Bode Plot,确实如它们的名字所述“低通高阻”或者“高通低阻”。
之后我们会通过Bode Plot来理解传递函数的
零极点对系统响应的影响,以及为什么微分信号会放大噪音等等这些问题。这一切都会从Bode Plot的绘制开始说起。
Reference:
[1] G.F. Franklin, J.D. Powell, A.Emami-Naeini, Feedback Control of Dynamic Systems, 7th Edition, 2014, Pearson
[2]
胡寿松,自动控制原理(第六版),2013,科学出版社
若有纰漏,烦请指出。 转载还请私信联系,请勿私自转载。O(∩_∩)O

关于博主
an actually real engineer
通信工程专业毕业,7年开发经验
技术栈:
精通c/c++
精通golang
熟悉常见的脚本,js,lua,python,php
熟悉电路基础,嵌入式,单片机
耕耘领域:
服务端开发
嵌入式开发
>gin接口代码CURD生成工具
sql ddl to struct and markdown,将sql表自动化生成代码内对应的结构体和markdown表格格式,节省宝贵的时间。
qt .ui文件转css文件
duilib xml 自动生成绑定控件代码
协议调试器
基于lua虚拟机的的协议调试器软件 支持的协议有:
串口
tcp客户端/服务端
udp 组播/udp节点
tcp websocket 客户端/服务端
软件界面

使用例子: 通过脚本来获得接收到的数据并写入文件和展示在界面上
下载地址和源码
webrtc easy demo
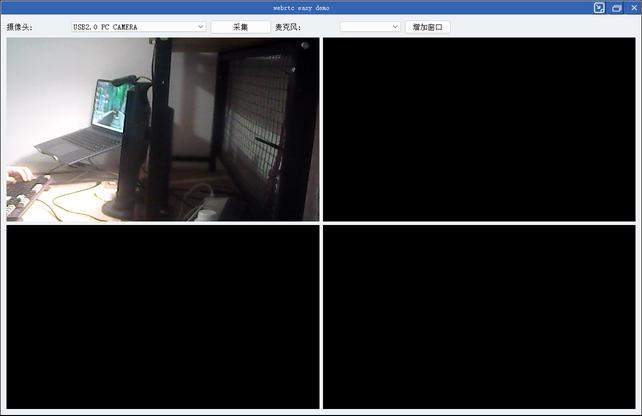
webrtc c++ native 库 demo 实现功能:
基于QT
webrtc摄像头/桌面捕获功能
opengl渲染/多播放窗格管理
janus meeting room
下载地址和源码
wifi,蓝牙 - 无线开关
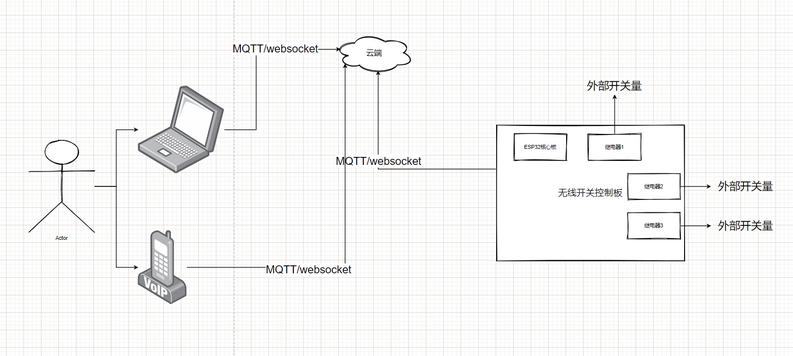
实现功能:
通过wifi/蓝牙实现远程开关电器或者其他电子设备
电路原理图:
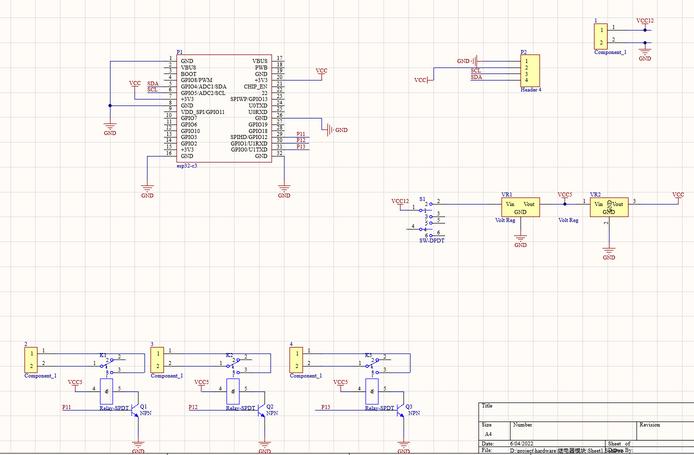
实物图:

深度学习验证工具
虚拟示波器
硬件实物图:

实现原理
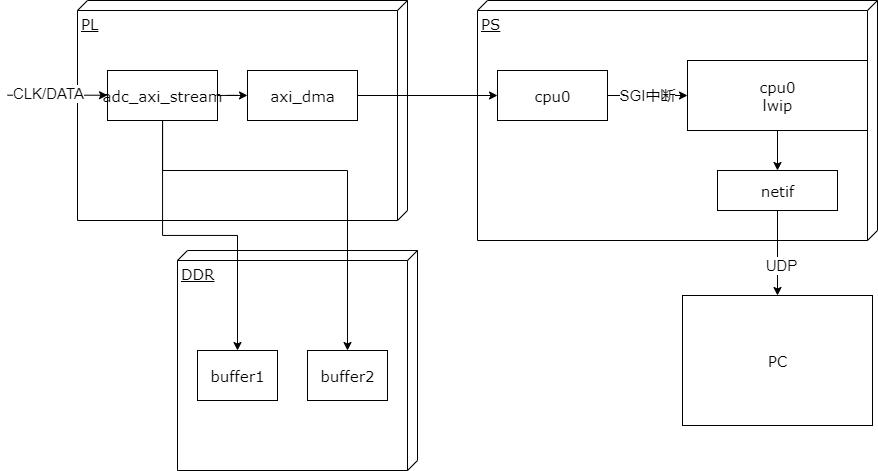
基本性能
采集频率: 取决于外部adc模块和ebaz4205矿板的以太网接口速率,最高可以达到100M/8 约为12.5MPS
上位机实现功能: 采集,显示波形,存储wave文件。
参数可运行时配置
上位机:

显示缓冲区大小可调
刷新率可调节
触发显示刷新可调节
又一个modbus调试工具
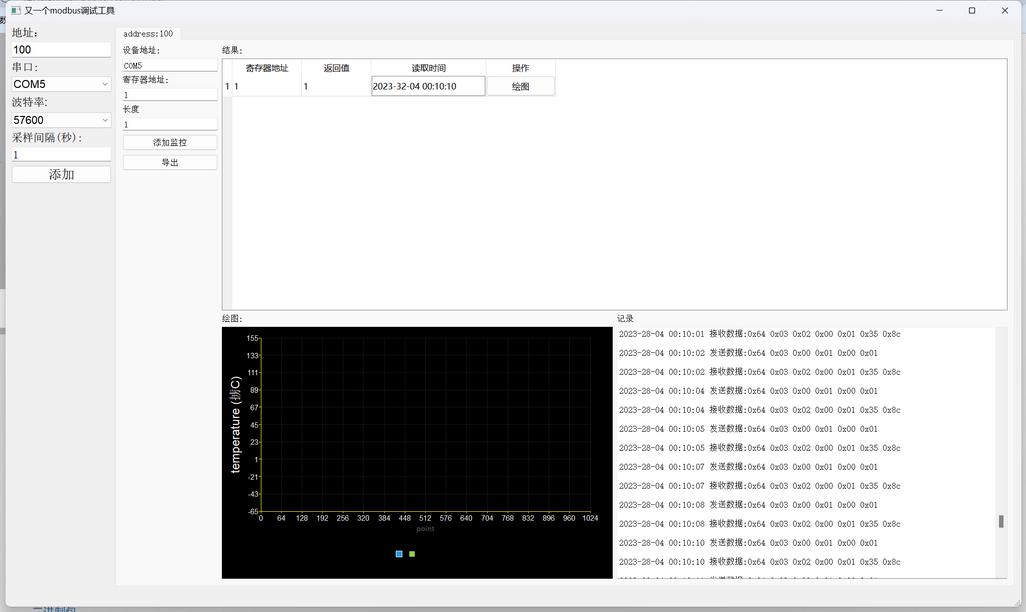
最近混迹物联网企业,发现目前缺少一个简易可用的modbus调试工具,本软件旨在为开发者提供一个简单modbus测试工具。
主打一个代码简单易修改。
特点:
1. 基于QT5
2. 基于libmodbus
3. 三方库完全跨平台,linux/windows。
开源plutosdr 板卡

1. 完全开源
2. 提高固件定制服务
3. 硬件售价450 手焊产量有线
测试数据
内部DDS回环测试

接收测试
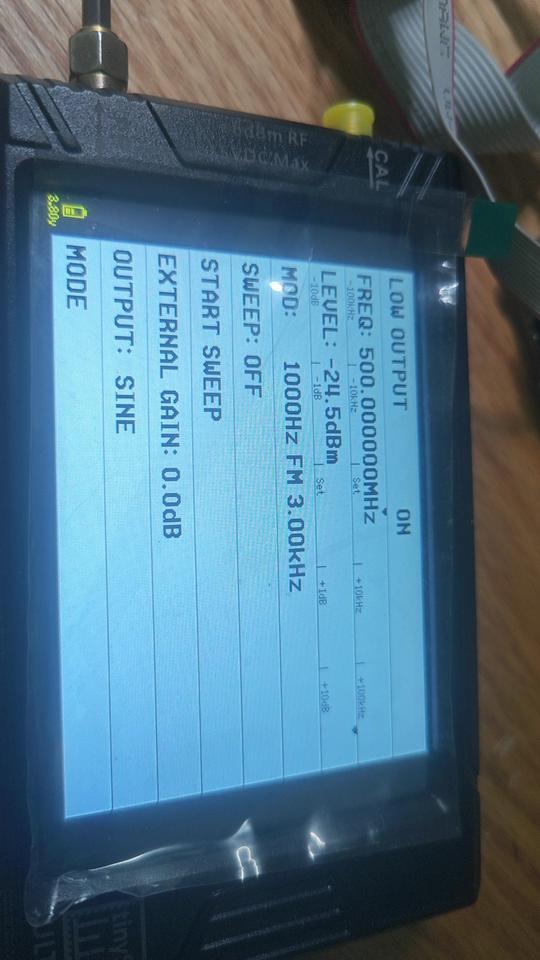
外部发送500MHZ FM波形
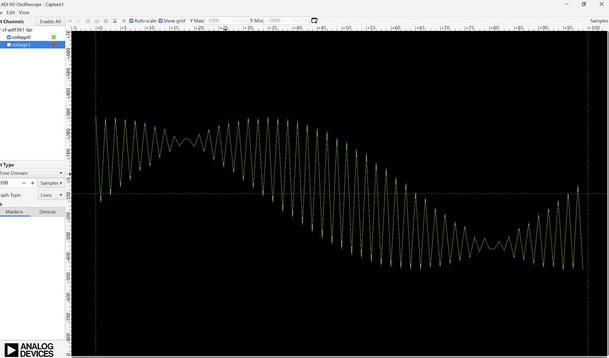
matlab测试

2TRX版本

大部分plutosdr应用场景都是讲plutosdr板卡作为射频收发器来使用。
实际上plutosdr板卡本身运行linux 操作系统。是具有一定脱机运算的能力。
对于一些微型频谱检测,简单射频信号收发等应用完全可以将应用层直接实现在板卡上
相较于通过网卡或者USB口传输具有更稳定,带宽更高等优点。
本开源板卡由于了SD卡启动,较原版pluto支持了自定义启动应用的功能。
提供了应用层开发SDK(编译器,buildroot文件系统)。
通过usb连接电脑,经过RNDIS驱动可以近似为通过网卡连接
(支持固件的开发定制)。
二次开发例子
```
all:
arm-linux-gnueabihf-gcc -mfloat-abi=hard --sysroot=/root/v0.32_2trx/buildroot/output/staging -std=gnu99 -g -o pluto_stream ad9361-iiostream.c -lpthread -liio -lm -Wall -Wextra -lrt
clean:
rm pluto_stream
版面分析即分析出图片内的具体文件元素,如文档标题,文档内容,文档页码等,本工具基于cnstd模型