永磁同步电机的稳定带载启动一直是业界研究的重点,不管是使用高频注入获取转子初始位置,还是使用各种“高级”的观测器能实现零速闭环启动,不能否认的是工业界目前使用最多且最可靠的仍然是转速开环、电流闭环的IF
控制策略,即所谓的强拖。该控制策略的优点在于不需要电机参数,启动稳定可靠,调参后基本能做到针对性负载的100%启动成功率,缺点在于它的带负载能力差,负载发生变化后需要重新调整参数。如果控制对象负载是基本固定不变的,使用IF控制策略不失为一种稳定可靠的启动策略,这也是它在工业界得到广泛应用的原因。在实际应用中算法是否高大大,复杂先进往往不是最重要的,稳定可靠,调参简单,移植方便则是决定是一种算法能否“流行“,得到应用的关键。那么IF控制策略背后的理论基础是什么呢?那就是“转矩—功角适应性”理论,理解好这个理论基础,不仅对IF控制,还对理解FOC整个控制过程都有非常大的帮助。
** 首先,看下功角的概念;**
功角又称为转矩角,它定义为为转子磁场与定子电流相量的夹角 $\delta$ ,如下的
向量图中的 $\delta$ 所示:
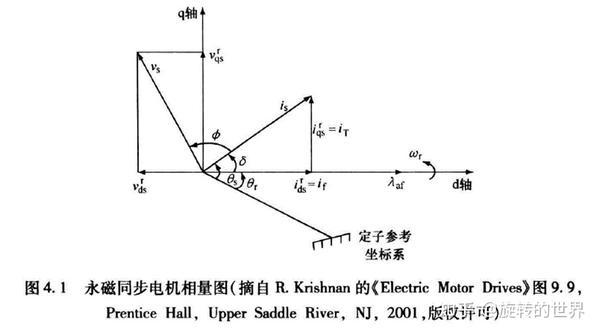
电机以 $\omega_{r}$ 速度正方向旋转时, $i_{s}$ 是定子电流方向,d轴方向是转子磁场方向, $i_{s}$ 投影在旋转坐标系d轴和q轴上产生的分量分别是电流 $i_{ds}^{r}$ 和 $i_{qs}^{r}$ ,$i_{ds}^{r}$ 沿着旋转的d轴方向仅能用于产生磁通,因而又被称为定子电流的磁通分量 $i_{f}$ , 转子磁通的剩余部分由
永磁体产生 $\lambda_{af}$ . $i_{qs}^{r}$与转子磁通正交,用于产生转矩, 推动电机旋转,因此又被称为定子电流的转矩分量 $i_{T}$ 。
显而易见,$i_{ds}^{r}$ 、 $i_{qs}^{r}$ 和$i_{s}$ 的关系满足公式:
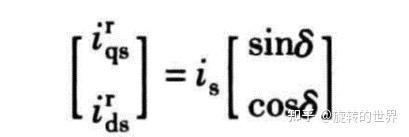
功角,即可以理解这个角度的大小是和做功大小是有直接关系的,角度越大,在同样 $i_{s}$ 条件下,$i_{qs}^{r}$值越大,输出力矩越大,这也是这个角度又被命名为转矩角的原因。FOC(
磁场定向控制)从本质上说就是功角等于90度的控制策略,当功角等于90度时,$i_{qs}^{r}$值达到最大,$i_{ds}^{r}$等于0,输出的电磁力矩达到最大。
其次,看下IF控制策略中, 功角怎么体现;
IF控制策略的控制框图如下:
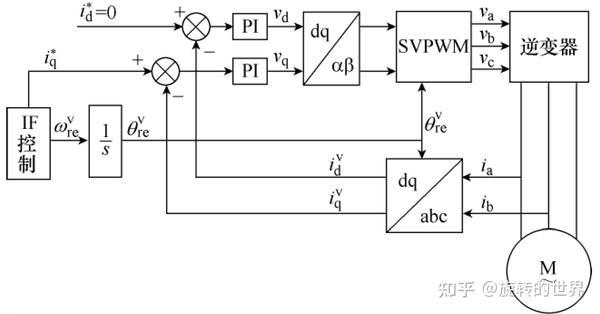
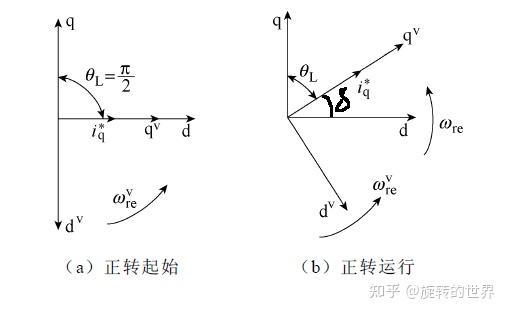
IF控制策略是一种转速开环、电流闭环的方式,输出一个合适的q
轴电流设定值 $i_{q}^{*}$ , 同时对转速给定信号 $\omega_{re}^{v}$ 积分,产生自动累加的角度信号 $\theta^{v}$ , 因为电流值 $i_{q}$ , 角度 $\theta$ 都是在一个虚拟的旋转坐标系下产生,这个虚拟坐标系可以理解为是软件施加向量所在的dq坐标系,用上标加 $v$ 为$d^{v}$ $q^{v}$来表示虚拟坐标系,它与转子的真实位置所在的 $dq$ 坐标系之间必然存在
相位差,这个相位差定义为 $\theta_{L}$ , 此时与$\theta_{L}$ 互补的角度就是功角,即 $\delta$ = pi/2 – $\theta_{L}$。它们之间的
相位关系可以从下面的向量图中看出。这也符合前面关于功角的定义,定子电流加在 $q^{v}$ 轴上,$q^{v}$轴与转子磁场方向d轴的夹角即为功角。
** 接着,看下”转矩—功角自适应“理论在IF控制策略怎么起作用;**
三相永磁同步电机的
电磁转矩方程是:
$T_{e} = 1.5 Pi_{q}\left[\psi_{r} + i_{d} (L_{d}-L_{q}) \right]$
式中, P为电机极对数; $\psi_{r}$ 为永磁体磁链;Ld 和Lq分别为直轴电感和交轴电感; 转矩方程分为两部分,第一项是电机定子电流和永磁体磁场之间产生的电磁转矩,第二项是由于转子
凸极效应产生的磁阻转矩。在IF控制策略下, $i_{d},i_{q}$ 就需要替换成虚拟坐标系值在转子坐标系下投影的分量,即方程变为:
$T_{e} = 1.5 Pi_{q}^{}cos\theta_{L}\left[\psi_{r}+ i_{q}^{}sin\theta_{L}(L_{d}-L_{q}) \right]$
表贴式 PMSM 中直流电感等于交轴电感,在有一定凸极率的内埋式PMSM 中直轴电感小于交轴电感,由于电感值通常较小,因此电磁转矩公式可以简化成:
$T_{e} \approx 1.5 Pi_{q}^{*}cos\theta_{L}\psi_{r}$
由此可见,除了值不变的极对数P和磁链 $\psi_{f}$ 外,这个公式中能决定输出力矩大小是施加q轴电流大小和虚拟$d^{v}$ $q^{v}$坐标系和真实 $dq$ 轴坐标系之间的相位差 $\theta_{L}$ ;
而电机的运动方程可表示为:
$T_{e} -T_{L} = J\frac{d\omega_{r}}{dt} =J\frac{d\theta^{2}_{r}}{dt}$
式中$T_{e}$是电磁转矩,$T_{L}$是负载转矩,$J$ 是电机的
转动惯量; $\omega_{r}$ 为转子角速度,$\theta_{r}$为转子角度;
以电机正转为例,对IF控制的“转矩-功角自适应”理论进行分析。结合向量图:
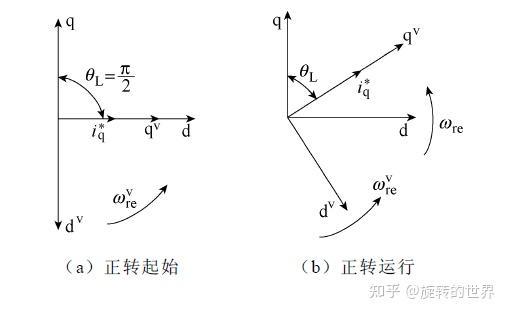
当电机进入稳态时,电磁转矩e 和负载转矩L 相等,加速度这一项等于0,定子磁场和转子磁场旋转速度相等,虚拟坐标系和转子坐标系相位差固定,功角固定。功角大小自适应到一个适当的值,使得Te输出值等于TL。
当负载转矩TL突然变大,转子转速下降,加速度这一项为负值,虚拟同步坐标系角度不变,转子同步坐标系角度滞后,导致两坐标系的相位差 $\theta_{L}$ 变小,进而导致电磁转矩e 输出提高,最后在一切都不变的情况下,在一个新的变小的相位差角度 $\theta_{L}$ 下,Te输出值等于TL。
当负载转矩TL突然变小,转子转速上升,加速度这一项为正值,虚拟同步坐标系角度不变,转子同步坐标系角度超前,导致两坐标系的相位差 $\theta_{L}$ 变大,进而导致电磁转矩e 输出降低,最后在一切都不变的情况下,在一个新的变大的相位差角度 $\theta_{L}$ 下,Te输出值等于TL。
$\theta_{L}$ 的变化与功角 $\delta$ 的变化相反,$\theta_{L}$变化与电磁力矩变化是负相关的,功角的变化与力矩变化是正相关的。 即负载力矩增大或减小时,功角自适应增大或减小,增加或减小电磁力矩,以达到新的平衡,这就是“转矩-功角自适应”特性 ,这个变化过程是自动完成的,自适应外界负载变化的,不需要在控制上作任何的处理,只需要整个过程仍然保证电流IF
闭环控制中输出电流幅值的稳定和自加角度的正确。
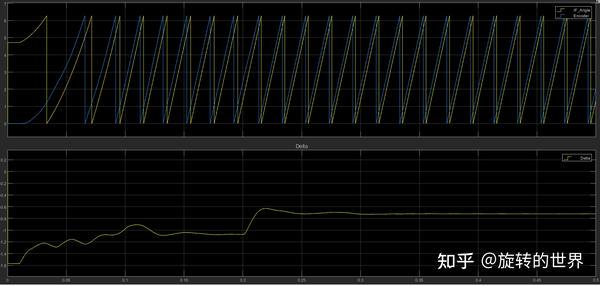
再从仿真上看下强拖加速和
稳定过程,电磁力矩、负载力矩、转速,相位差$\theta_{L}$这些量的变化,会有更深刻的理解。给2.0A的 $i_{q}$ 电流,IF控制策略强拖电机从0转速推动到600rpm后稳定。
电磁力矩 $T_{e}$ 和负载力矩 $T_{L}$ 的变化:加速过程 $T_{e}$ 基本大于 $T_{L}$ ,速度稳定后 $T_{e}$ 围绕 $T_{L}$ 波动
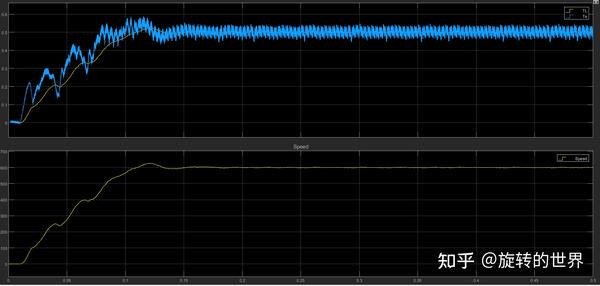
虚拟坐标系和转子坐标系相位差 $\theta_{L}$ 的变化: 从图中看也是符合理论分析的,从初始值的pi/2渐渐缩小到某一值稳定。
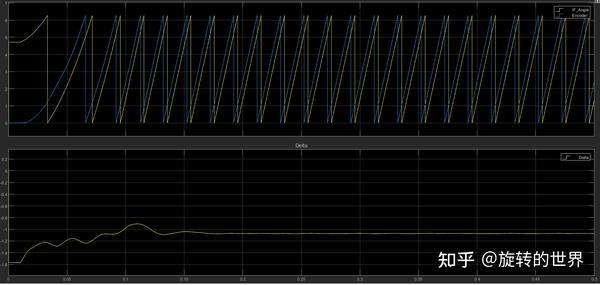
在0.2秒突然增加0.3NM的负载,发现相位差 $\theta_{L}$变小,平衡后重新达到一个稳定状态。
了解了“转矩-功角自适应”自适应原理,对我们指导实践有什么帮助呢?帮助太多了,这里简要列举几点。
** 1. 强拖过程中电流幅值和加速度的设计;**
电流给定 $i_{q}^{*}$ 幅值越大,则稳态情况下相位差 $\theta_{L}$ 也越大,越接近π/2。相位差越大则电机的电磁转矩储备越大,电机抵抗负载扰动的能力越强。电流给定$i_{q}^{*}$幅值越小,则稳态情况下相位差 $\theta_{L}$ 也越小,越接近 $0^{。}$ 。相位差越小则电机的电磁转矩储备越小,电机抵抗负载扰动的能力越弱。电流幅值的设计原则是在大于负载转矩 $T_{L}$ 的前提下,电流给定 $i_{q}^{*}$ 幅值尽可能大,以适应不同的各种
启动工况。
在电流给定幅值一定的情况下,θL=0°时电机的电磁转矩达到最大值。设电机加速度为ω,则加速度ω应该满足:
$Kw< \frac{1}{J}(1.5 Pi_{q}^{*}\psi_{r}-T_{Lmax})$
式中, $T_{Lmax}$ 为电机的最大负载转矩。在IF 控制中,电机的加速度越大,则电机的抗扰动能力越弱,电机出现失步的概率越大。
** 2. FOC过程运行过程上加速不到额定负载;**
如果在FOC运行过程中加力矩无法加到额定负载,那么很大的一种可能就是估算的角度是不正确的,那样就会造成使用的角度和转子的角度有一个相位差,从前面的分析来看,实际输出的有效力矩将大打折扣。
3 . 强拖到切换速度闭环过程中怎么保证平稳顺滑,电流不突变。
这一点可以参考以下文章:
FOC控制中如何实现电机启动过程中速度稳定切换119 赞同 · 126 评论文章
** 4. 电机失步分析**
相位差 $\theta_{L}$ 的变化范围可以在0到pi变化。
加速时,力矩电流需求不能超过 $i_{Tmax} = Iq *cos 0 = Iq$ ,否则电机会失步;
减速时,力矩电流需求不能超过 $i_{Tmax} = Iq *cos pi = -Iq$ ,否则电机会失步;
** 5. 定位初始角度**
如果要使启动初始时刻的电磁力矩输出从0开始,当使用Iq电流定位时,角度要从-pi/2开始;当使用Id电流定位时,角度可以从0度开始。
以上所有的实践过程都可以在
仿真模型中得到预演,在同名闲鱼账号中更新了”定位+ 电流闭环强拖+ 角度渐变切换+ 速度电流双闭环+ 无传感器角度估算SMO+ PLL 控制方式 Simulink 仿真模型"。 相比上一版,增加和更新了以下功能:1. 定位;2. 状态的切换使用stateflow,整个模型结构清淅简单 3.修正了部分原来滑模观测器的错误,使内嵌和表贴电机通用。已经购买的老客户将赠送更新后的模型。
全文用心完成,欢迎评论和点赞。
参考文献:IF控制结合滑模观测器的永磁同步电机无
位置传感器复合控制策略,刘计龙。

关于博主
an actually real engineer
通信工程专业毕业,7年开发经验
技术栈:
精通c/c++
精通golang
熟悉常见的脚本,js,lua,python,php
熟悉电路基础,嵌入式,单片机
耕耘领域:
服务端开发
嵌入式开发
>gin接口代码CURD生成工具
sql ddl to struct and markdown,将sql表自动化生成代码内对应的结构体和markdown表格格式,节省宝贵的时间。
qt .ui文件转css文件
duilib xml 自动生成绑定控件代码
协议调试器
基于lua虚拟机的的协议调试器软件 支持的协议有:
串口
tcp客户端/服务端
udp 组播/udp节点
tcp websocket 客户端/服务端
软件界面

使用例子: 通过脚本来获得接收到的数据并写入文件和展示在界面上
下载地址和源码
webrtc easy demo
webrtc c++ native 库 demo 实现功能:
基于QT
webrtc摄像头/桌面捕获功能
opengl渲染/多播放窗格管理
janus meeting room
下载地址和源码
wifi,蓝牙 - 无线开关
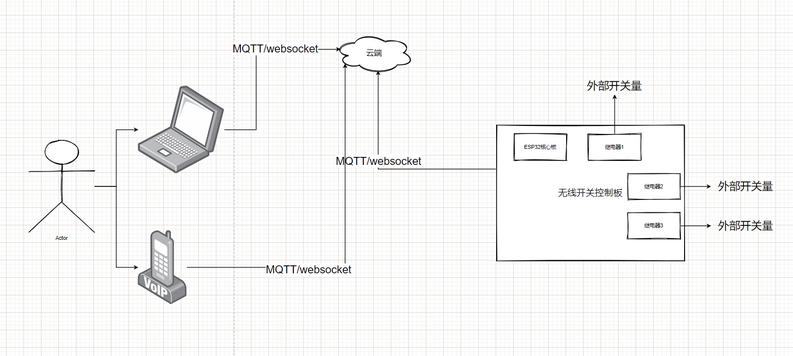
实现功能:
通过wifi/蓝牙实现远程开关电器或者其他电子设备
电路原理图:
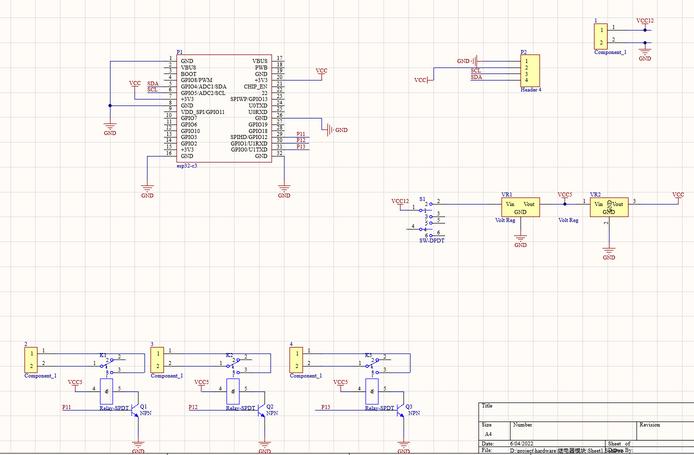
实物图:

深度学习验证工具
虚拟示波器
硬件实物图:

实现原理
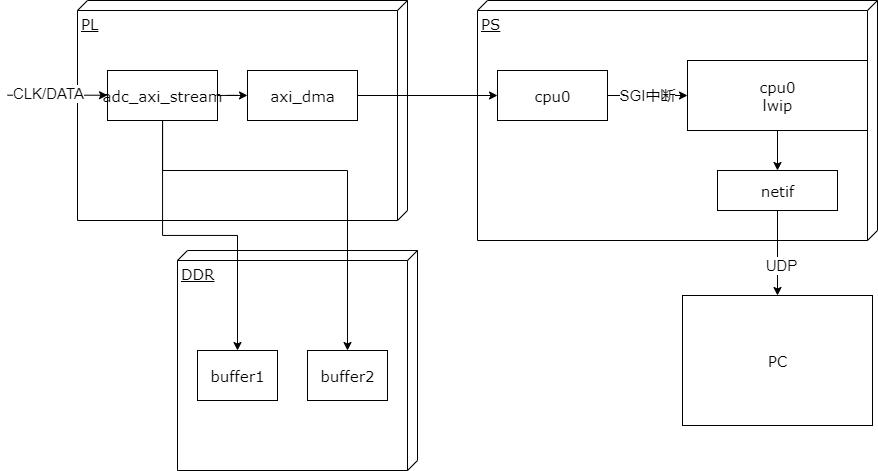
基本性能
采集频率: 取决于外部adc模块和ebaz4205矿板的以太网接口速率,最高可以达到100M/8 约为12.5MPS
上位机实现功能: 采集,显示波形,存储wave文件。
参数可运行时配置
上位机:

显示缓冲区大小可调
刷新率可调节
触发显示刷新可调节
又一个modbus调试工具
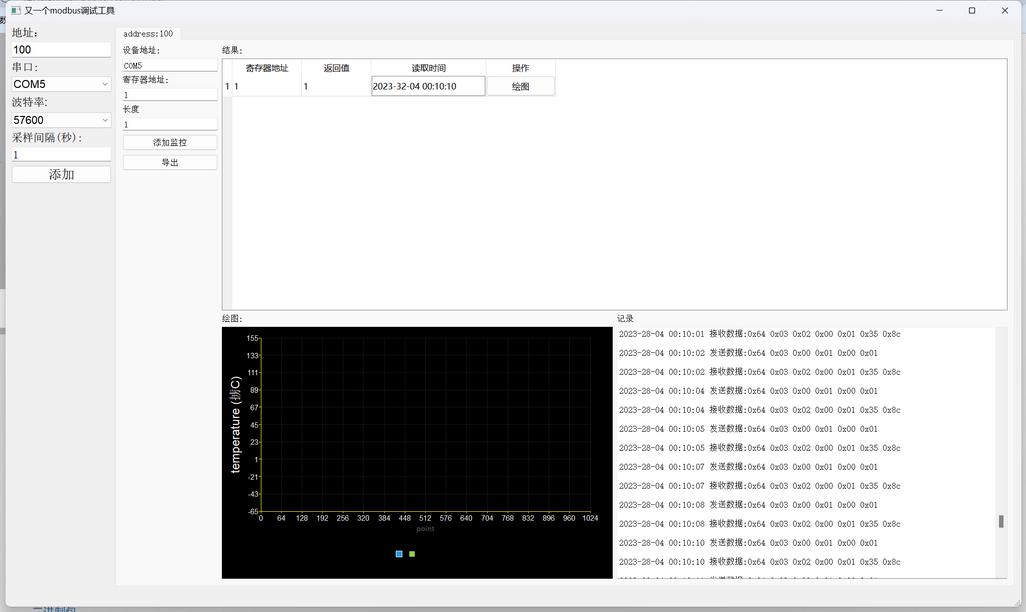
最近混迹物联网企业,发现目前缺少一个简易可用的modbus调试工具,本软件旨在为开发者提供一个简单modbus测试工具。
主打一个代码简单易修改。
特点:
1. 基于QT5
2. 基于libmodbus
3. 三方库完全跨平台,linux/windows。
开源plutosdr 板卡

1. 完全开源
2. 提高固件定制服务
3. 硬件售价450 手焊产量有线
测试数据
内部DDS回环测试

接收测试
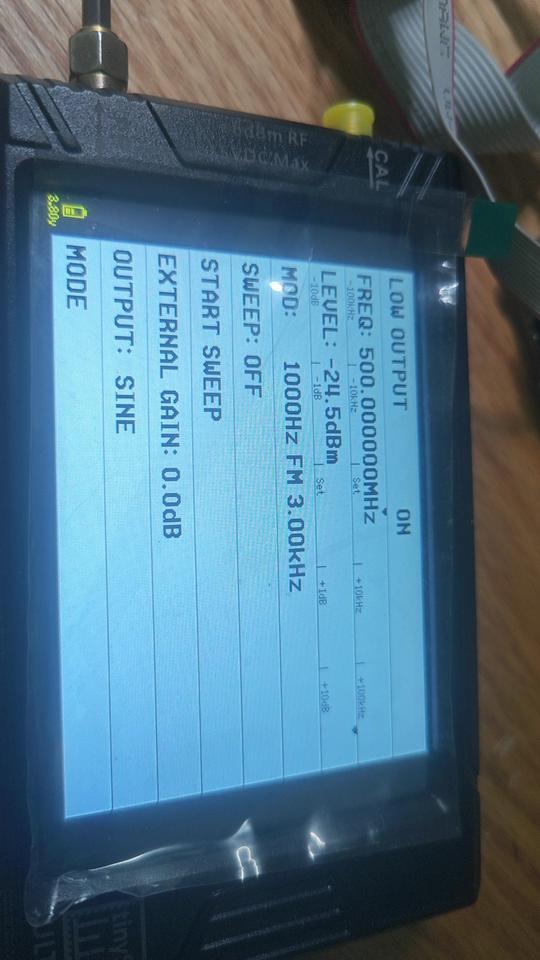
外部发送500MHZ FM波形
matlab测试

2TRX版本

大部分plutosdr应用场景都是讲plutosdr板卡作为射频收发器来使用。
实际上plutosdr板卡本身运行linux 操作系统。是具有一定脱机运算的能力。
对于一些微型频谱检测,简单射频信号收发等应用完全可以将应用层直接实现在板卡上
相较于通过网卡或者USB口传输具有更稳定,带宽更高等优点。
本开源板卡由于了SD卡启动,较原版pluto支持了自定义启动应用的功能。
提供了应用层开发SDK(编译器,buildroot文件系统)。
通过usb连接电脑,经过RNDIS驱动可以近似为通过网卡连接
(支持固件的开发定制)。
二次开发例子
```
all:
arm-linux-gnueabihf-gcc -mfloat-abi=hard --sysroot=/root/v0.32_2trx/buildroot/output/staging -std=gnu99 -g -o pluto_stream ad9361-iiostream.c -lpthread -liio -lm -Wall -Wextra -lrt
clean:
rm pluto_stream
版面分析即分析出图片内的具体文件元素,如文档标题,文档内容,文档页码等,本工具基于cnstd模型