关于博主
an actually real engineer
通信工程专业毕业,7年开发经验
技术栈:
精通c/c++
精通golang
熟悉常见的脚本,js,lua,python,php
熟悉电路基础,嵌入式,单片机
耕耘领域:
服务端开发
嵌入式开发
>gin接口代码CURD生成工具
sql ddl to struct and markdown,将sql表自动化生成代码内对应的结构体和markdown表格格式,节省宝贵的时间。
qt .ui文件转css文件
duilib xml 自动生成绑定控件代码
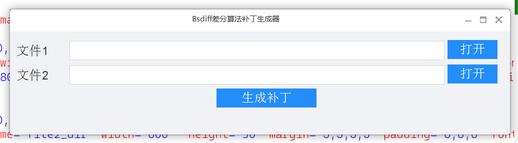
协议调试器
基于lua虚拟机的的协议调试器软件 支持的协议有:
串口
tcp客户端/服务端
udp 组播/udp节点
tcp websocket 客户端/服务端
软件界面

使用例子: 通过脚本来获得接收到的数据并写入文件和展示在界面上
下载地址和源码
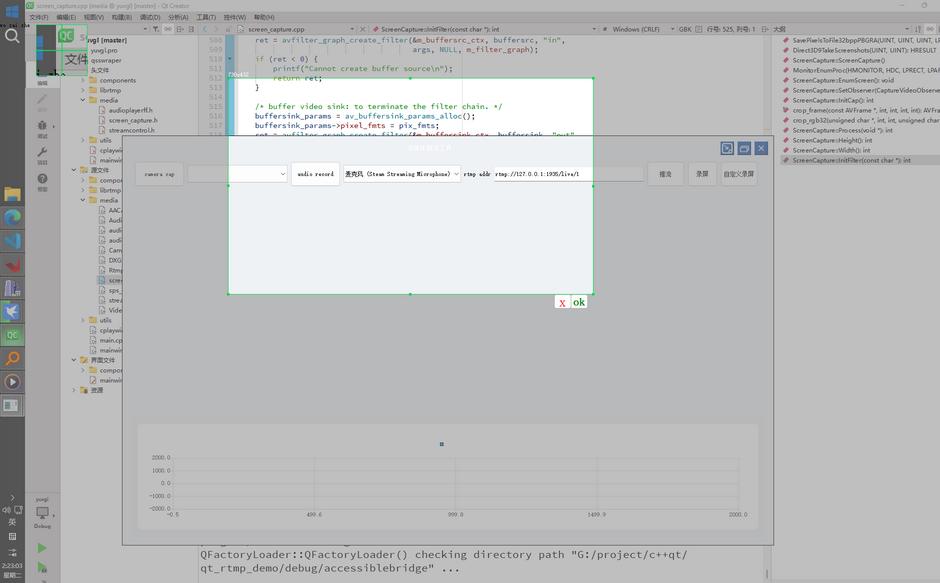
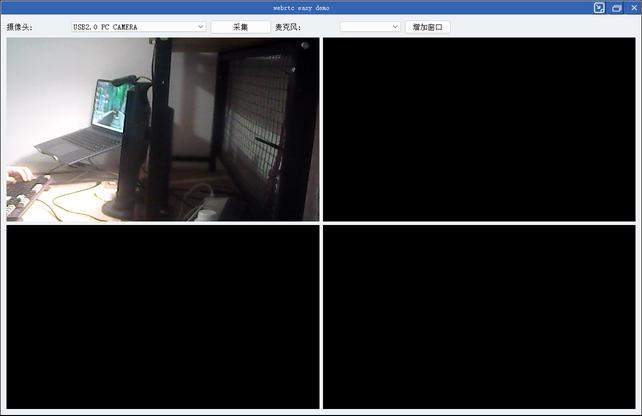
webrtc easy demo
webrtc c++ native 库 demo 实现功能:
基于QT
webrtc摄像头/桌面捕获功能
opengl渲染/多播放窗格管理
janus meeting room
下载地址和源码
wifi,蓝牙 - 无线开关
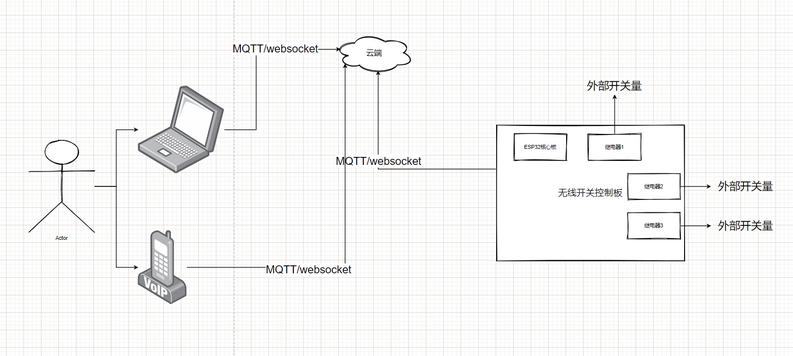
实现功能:
通过wifi/蓝牙实现远程开关电器或者其他电子设备
电路原理图:
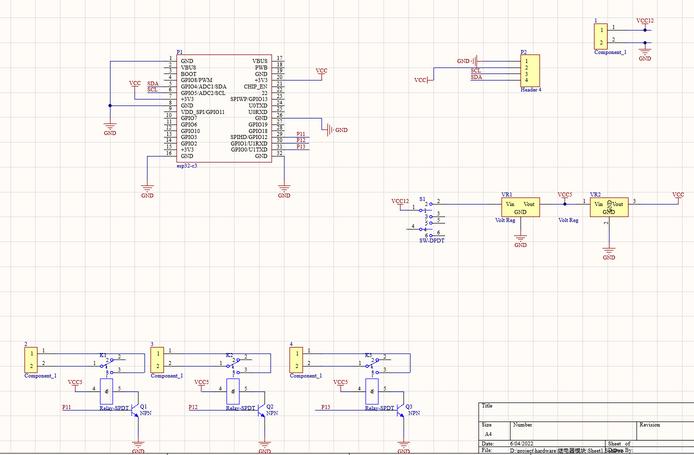
实物图:

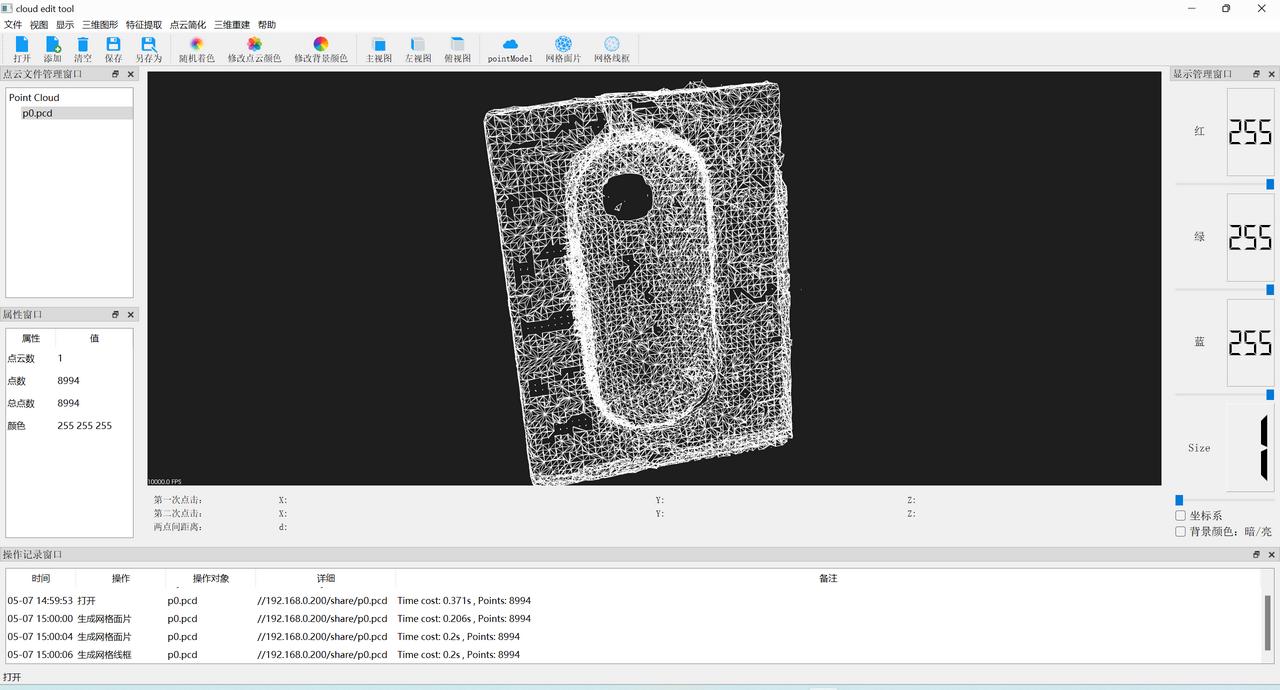
深度学习验证工具
虚拟示波器
硬件实物图:

实现原理
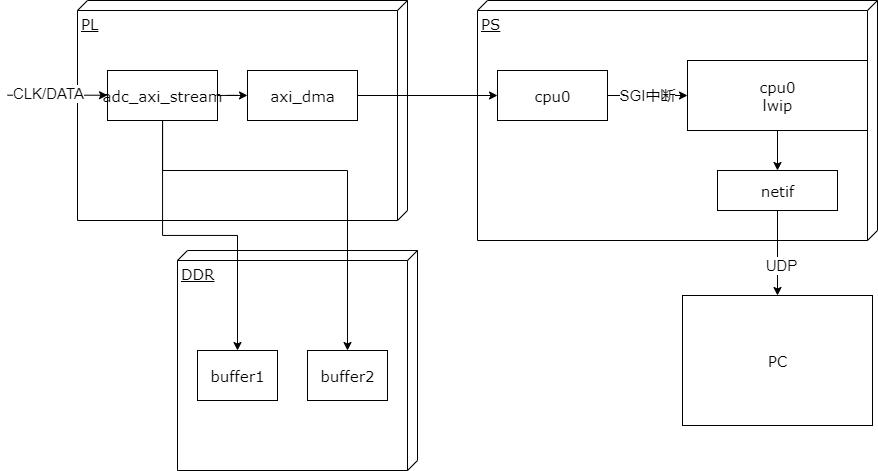
基本性能
采集频率: 取决于外部adc模块和ebaz4205矿板的以太网接口速率,最高可以达到100M/8 约为12.5MPS
上位机实现功能: 采集,显示波形,存储wave文件。
参数可运行时配置
上位机:

显示缓冲区大小可调
刷新率可调节
触发显示刷新可调节
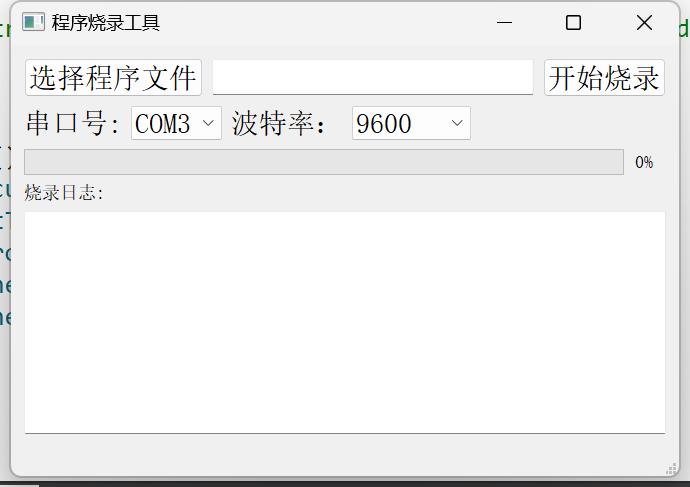
又一个modbus调试工具
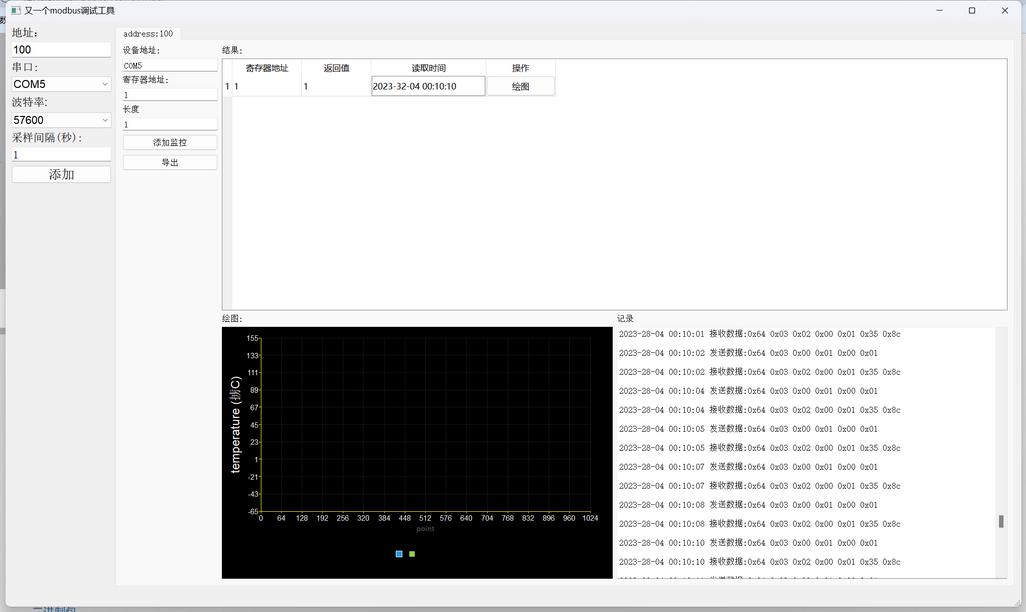
最近混迹物联网企业,发现目前缺少一个简易可用的modbus调试工具,本软件旨在为开发者提供一个简单modbus测试工具。 主打一个代码简单易修改。 特点:
1. 基于QT5
2. 基于libmodbus
3. 三方库完全跨平台,linux/windows。
开源plutosdr 板卡

1. 完全开源
2. 提高固件定制服务
3. 硬件售价450 手焊产量有线
测试数据
内部DDS回环测试

接收测试
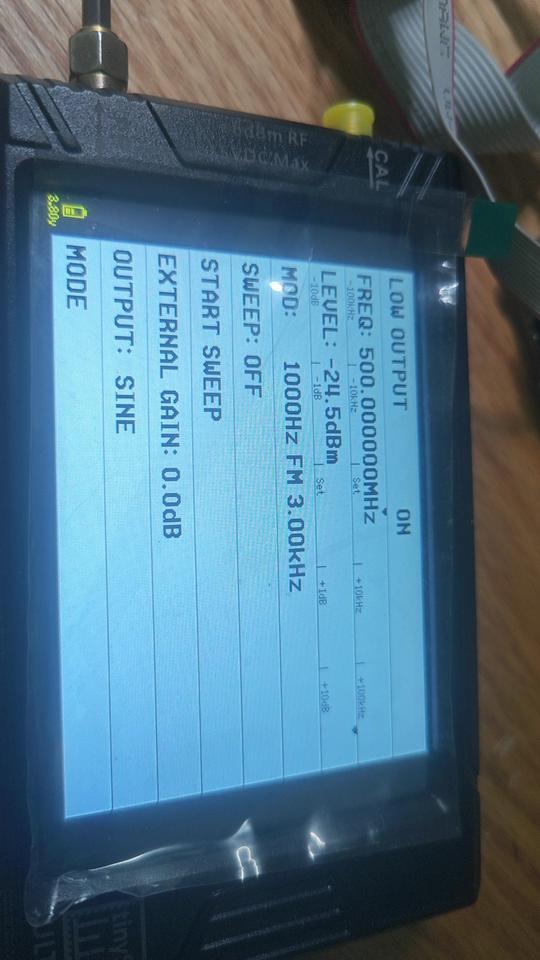
外部发送500MHZ FM波形
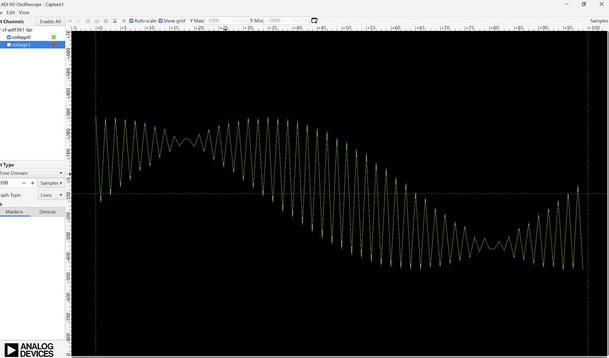
matlab测试

2TRX版本

大部分plutosdr应用场景都是讲plutosdr板卡作为射频收发器来使用。 实际上plutosdr板卡本身运行linux 操作系统。是具有一定脱机运算的能力。 对于一些微型频谱检测,简单射频信号收发等应用完全可以将应用层直接实现在板卡上 相较于通过网卡或者USB口传输具有更稳定,带宽更高等优点。 本开源板卡由于了SD卡启动,较原版pluto支持了自定义启动应用的功能。 提供了应用层开发SDK(编译器,buildroot文件系统)。 通过usb连接电脑,经过RNDIS驱动可以近似为通过网卡连接 (支持固件的开发定制)。
二次开发例子
``` all: arm-linux-gnueabihf-gcc -mfloat-abi=hard --sysroot=/root/v0.32_2trx/buildroot/output/staging -std=gnu99 -g -o pluto_stream ad9361-iiostream.c -lpthread -liio -lm -Wall -Wextra -lrt clean: rm pluto_stream
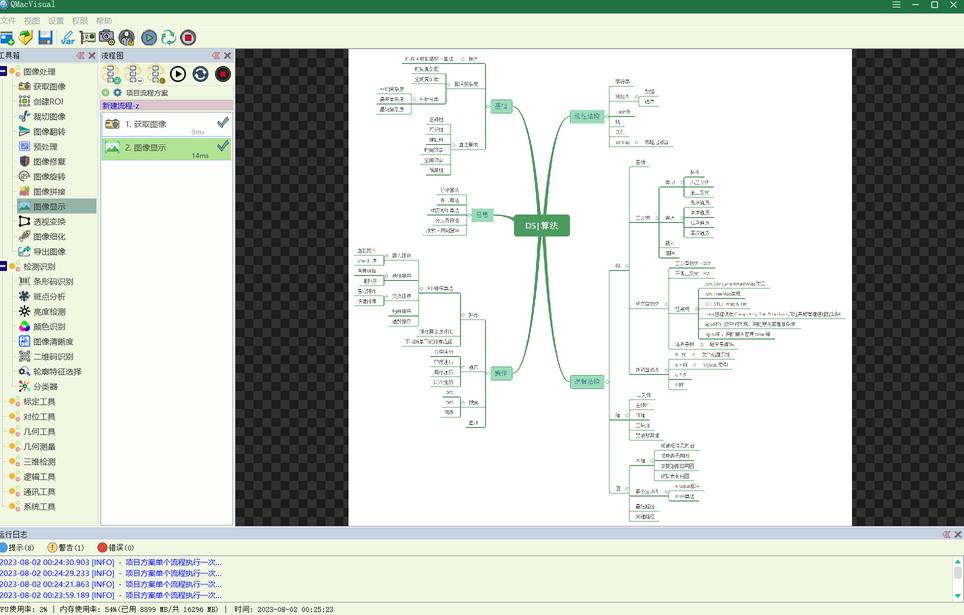
版面分析即分析出图片内的具体文件元素,如文档标题,文档内容,文档页码等,本工具基于cnstd模型